Точки в естественных координатных осях
Условие задачи.
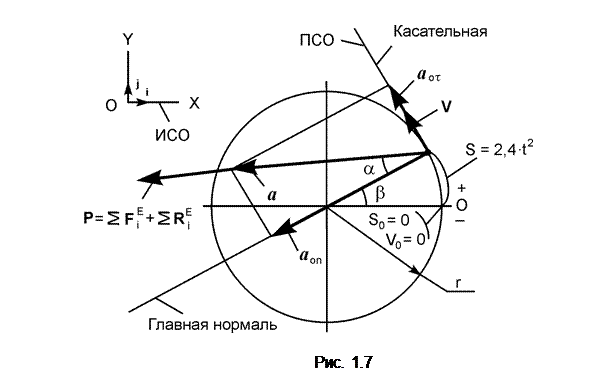
Материальная точка массой m = 1,2 кг движется по окружности радиуса r = 1 м на гладкой горизонтальной поверхности согласно уравнению S = 2,4·t2 (рис. 1.7). Заданы начальные условия движения: S0 = 0; V0 = 0. Определить модуль равнодействующей сил, приложенных к материальной точке в момент времени t1 = 1 c.
Решение.
1. На рис. 1.7 изобразим материальную точку в произвольный момент времени.
2. В эту точку поместим начало координат ПСО.
3. Орт τ направлен в сторону возрастания дуговой координаты S, а орт n направлен к центру кривизны траектории движения. Этим центром является центр окружности. Радиус ρ кривизны траектории движения точки равен радиусу окружности ρ = r.
4. Покажем на рис. 1.7 начальные условия движения. По условиям задачи S0 = 0; V0=0.
5. Согласно условию задачи к точке приложены активные силы G и F1 и реакция N гладкой поверхности. Поскольку рис. 1.7 изображен в ортогональных проекциях, то силы G и Nперпендикулярны опорной поверхности точки и, следовательно, на рисунке не видны. Основное уравнение динамики для решаемой задачи имеет вид
m·a = ΣFiE + ΣRiE = G+ F1+ N.
 |
6. Запишем дифференциальные уравнения движения точки в естественных координатных осях.
m· 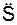 = Σ
= Σ 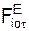 + Σ
+ Σ 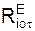 = F1·sin(α); (1)
= F1·sin(α); (1)
m· 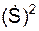 /ρ = Σ
/ρ = Σ 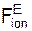 + Σ
+ Σ 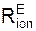 = F1·cos(α); (2)
= F1·cos(α); (2)
Σ 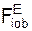 + Σ
+ Σ 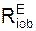 = 0 = – G + N. (3)
= 0 = – G + N. (3)
Из уравнения (3) имеем N = G = m·g = 1,2·9,81 = 11,772 H.
7. По заданному уравнению S = 2,4·t2 определим проекцию 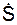 скорости V и проекцию
скорости V и проекцию 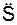 ускорения точки на касательную.
ускорения точки на касательную.
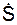 = 4,8·t;
= 4,8·t; 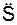 = 4,8 м/с2.
= 4,8 м/с2.
8. Найденные проекции 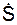 ,
, 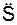 подставим в уравнения (1), (2). Получим:
подставим в уравнения (1), (2). Получим:
m·(4,8) = F1·sin(α); (1I)
m·(4,8·t)2/r = F1·cos(α). (2I)
9. Согласно уравнениям (1I), (2I) имеем:
Poτ = F1·sin(α); Pon = F1·cos(α),
где Poτ, Pon – проекции равнодействующей Р = G+ F1 + Nактивных сил и реакций внешних связей, приложенных к точке, на координатные оси ПСО. Тогда:
Poτ = m·(4,8); (1II)
Pon = m·(4,8·t)/r. (2II)
Определим значения P oτ и Pon в момент времени t1.
Poτ(t1) = 1,2·4,8 = 5,76 H;
Pon(t1) = m·(4,8·t1) = 1,2·4,8·1 = 5,76 H.
10. Определим модуль Р равнодействующей в момент времени t1.
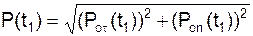 =
=
= 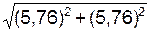 = 8,145 Н.
= 8,145 Н.
11. Для ориентации вектора Р в пространстве определим направляющие косинусы и величину угла α, составленного направлением равнодействующей силы Р и ортом τ.
cos(P(t1), τ) = Poτ(t1)/P(t1) = 5,76/8,145 = 0,707.
α = arcos(0,707) = 45o.
12. Определим положение точки на траектории её движения в момент времени t1 и зафиксируем это положение центральным углом β.
S(t1) = 2,4·(t1)2 = 2,4·12 = 2,4 м;
β = S(t1)/r = 2,4/1 = 2,4 рад.
В градусной мере β = (2,4/3,14)·180о = 137,579о.
Полученные результаты расчётов проиллюстрируем рис. 1.8.
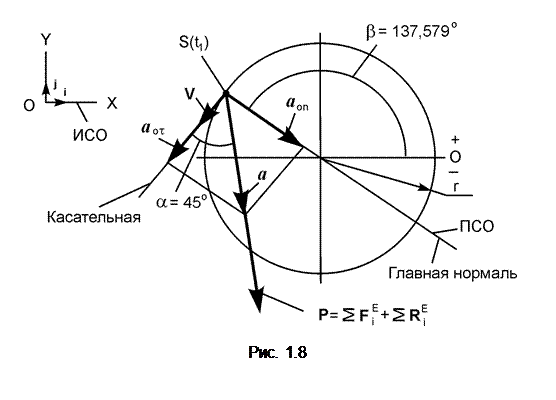 |
Таким образом, задача решена. Ответы на вопросы получены.
Дата добавления: 2015-05-30; просмотров: 1005;
