Свободные колебания материальной точки
Свободные колебания происходят под действием постоянной системы сил и восстанавливающей силы.
Для получения дифференциальных уравнений колебательного движения точки воспользуемся расчётной схемой, приведённой на рис. 2.1,б.
Согласно рис. 2.1,б на точку действует постоянная система сил (G, N) и восстанавливающая сила Fyn. Дифференциальные уравнения движения точки имеют вид:
m·  = Σ
= Σ 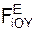 + Σ
+ Σ 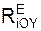 = – Fyn = – c·Δ = – c·Y;
= – Fyn = – c·Δ = – c·Y;
m· 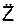 = Σ
= Σ 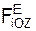 + Σ
+ Σ 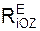 = – G + N.
= – G + N.

В этих уравнениях  ,
, 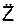 – проекции ускорения a соответственно на координатные оси OY и OZ. Поскольку
– проекции ускорения a соответственно на координатные оси OY и OZ. Поскольку 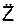 = 0, то имеем N = G = m·g. Таким образом, силы G и N образуют уравновешенную систему сил и, следовательно, эта система сил не влияет на параметры движения точки. Исходя из этого, расчётная схема для определения дифференциального уравнения движения точки упрощается (рис. 2.2).
= 0, то имеем N = G = m·g. Таким образом, силы G и N образуют уравновешенную систему сил и, следовательно, эта система сил не влияет на параметры движения точки. Исходя из этого, расчётная схема для определения дифференциального уравнения движения точки упрощается (рис. 2.2).
Дифференциальное уравнение горизонтального движения точки представим в виде
 + (c/m)·Y = 0.
+ (c/m)·Y = 0.
Введем постоянный коэффициент k2 = 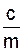 или k =.
или k =. 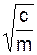 Тогда имеем
Тогда имеем
 + k2·Y = 0.
+ k2·Y = 0.
Это выражение называют дифференциальным уравнением свободных колебаний материальной точки.
Коэффициент k называют циклической частотой свободных колебаний, который измеряют в рад/с или в с-1. Физический смысл коэффициента k – число полных колебаний за время t = 2π = 6,28 c.
Общее решение этого дифференциального уравнения имеет два вида.
Первый вид:
Y = C1·cos(k·t) + C2·sin(k·t),
где С1, С2 – постоянные интегрирования, определяемые по начальным условиям движения.
Пусть при t0 = 0 точка имеет координату Y0 и проекцию 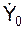 скорости V0 на ось ОY. Тогда уравнение свободных колебаний точки получит вид
скорости V0 на ось ОY. Тогда уравнение свободных колебаний точки получит вид
Y = 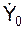 ·cos(k·t) +
·cos(k·t) + 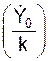 ·sin(k·t).
·sin(k·t).
Второй вид:
Y = A·sin(k·t + β),
где А и β – постоянные интегрирования; А – амплитуда свободных колебаний; (k·t + β) – фаза колебаний; β – начальная фаза колебаний.
По заданным начальным условиям движения точки (Y0, 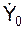 ) постоянные интегрирования определяют по следующей совокупности формул:
) постоянные интегрирования определяют по следующей совокупности формул:
A = 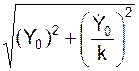 ;
;
sin(β) = 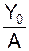 ; cos(β) =
; cos(β) = 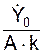 ; tg(β) =
; tg(β) = 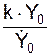 .
.
На рис. 2.3 представлен общий вид графика свободных колебаний точки.
 |
При изучении свободных (гармонических) колебаний широко используют понятия «амплитуда А», «период Т свободных колебаний».
Амплитуда свободных колебаний – величина наибольшего отклонения точки от положения статического равновесия.
Период свободных колебаний – отрезок времени, за который точка проходит положение статического равновесия в одном и том же направлении.
Период свободных колебаний определяют по формуле
T = 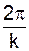 =
= 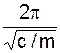 .
.
Анализ формулы показывает, что период свободных колебаний Т является постоянной величиной. С возрастанием массы m точки период Т увеличивается и соответственно уменьшается при увеличении коэффициента «с» жесткости пружины.
Следует отметить, что свободные колебания не затухают.
Для практических расчетов рекомендуется использовать формулу
Y = A·sin(k·t + β).
В инженерной практике довольно часто рассматривают колебательное движение тела, подвешенного на пружинах или установленного на них. Если начало системы отсчёта поместить в положение статического равновесия груза, то эти колебания также сводятся к свободным колебаниям точки, дифференциальное уравнение движения которой имеет стандартный вид  + k2·Y = 0 и, следовательно, стандартное решение.
+ k2·Y = 0 и, следовательно, стандартное решение.
Дата добавления: 2015-05-30; просмотров: 4801;
