Апериодическое движение точки

Рассмотрим второй вариант движения точки, при котором n = k. В таком варианте движение точки теряет колебательный характер и становится апериодическим. В этом случае общее решение дифференциального уравнения

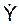+ 2n· + k²·Y = 0

имеет вид

Y = (e^-nt)·(C₁·t + C₂),

где С₁, С₂ – постоянные интегрирования, которые находятся по начальным условиям движения точки. Пусть при t₀ = 0 точка имеет координату Y₀ и проекцию 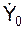скорости V₀ на ось ОY. С использование начальных условий уравнение апериодического движения точки имеет вид

Y = (e^-nt)·(Y₀+( 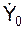+ n·Y₀)·t).

В зависимости от начальных условий материальная точка может совершать одно из движений, графики которых показаны на рис. 2.6 – 2.8. Эти графики соответствуют начальному отклонению точки от положения статического равновесия на величину 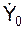> 0.

На рис. 2.6 показан график движения точки с начальной скоростью V₀, имеющей направление, совпадающее с направлением положительного отсчета координаты Y. Начальные условия этого движения изображены на рис. 2.4.

Так как проекция 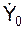> 0, то точка сначала удаляется от положения статического равновесия, а затем под действием восстанавливающей силы постепенно приближается к этому положению.

Графики (см. рис. 2.7 и 2.8) соответствуют движению точки с начальной скоростью V₀, направленной противоположно направлению отсчета координаты Y, т. е. имеем: Y₀ 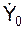> 0; < 0.

При достаточно большом значении начальной скорости V₀ точка может совершить один переход через положение статического равновесия и затем при обратном движении приближаться к этому положению (см. рис. 2.7).

При начальных условиях (Y₀ > 0; 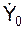= 0) график функции Y = f(t) имеет вид, приведенный на рис. 2.8.

Рассмотрим вариант движения точки, при котором n > k. При таком варианте точка совершает апериодическое движение, описываемое уравнением

Y = (e^-nt)·(C₁· 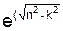^)·t + C₂· 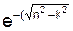^)·t),

где С₁, С₂ – постоянные интегрирования, определяемые по начальным условиям движения.

Графики движения точки в этом случае по существу не отличаются от графиков, приведенных на рис. 2.6 – 2.8.

Таким образом, если n = k или n > k, то точка совершает апериодическое движение. Такое движение называют также движением точки с большим сопротивлением внешней среды.