Силы и силы сопротивления движению

Рассмотрим движение материальной точки по гладкой горизонтальной поверхности, происходящее под действием постоянной системы сил, восстанавливающей силы и силы сопротивления движению, пропорциональной первой степени скорости (рис. 2.4).
Как и ранее, начало системы отсчёта поместим в положение статического равновесия точки. В этом положении пружина не деформирована, т. е. имеет длину l0. При оформлении рис. 2.4 используются рекомендации, приведённые в алгоритме решения вторых задач динамики точки.
Основное уравнение динамики в рассматриваемом случае имеет вид
m·a = ΣFiЕ + ΣRiЕ = G + N + Rc + Fyn,
где G – сила тяжести; N – нормальная реакция; Rc – сила сопротивления движению точки; Fyn – сила упругости пружины.
Так как силы G и N на кинематические параметры точки не влияют, то они на рис. 2.4 не показаны.
Сила Rc сопротивления движению точки зависит от внешней среды, в которой эта точка перемещается.
Рассмотрим вариант, при котором сила Rc пропорциональна первой степени скорости V точки. Примером такой силы является сопротивление воздуха при движении тела. В этом случае силу Rc определяют по формуле Rc = – α·V, где α – постоянный коэффициент пропорциональности, имеющий размерность [Н/(м/с)]. Коэффициент α численно равен силе сопротивления при скорости движения точки, равной 1 м/с. Сила сопротивления Rc всегда направлена в сторону, противоположную направлению скорости V.
Запишем дифференциальное уравнение горизонтального движения точки:
m·  = Σ
= Σ 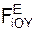 + Σ
+ Σ 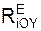 = – α·
= – α· 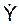 – c·Y.
– c·Y.
Это уравнение приведем к виду
 + (α/m)·
+ (α/m)· 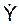 + (c/m)·Y = 0.
+ (c/m)·Y = 0.
Введем условные обозначения: α/m = 2n; c/m = k2. С учетом коэффициентов n, k дифференциальное уравнение движения приводится к стандартному виду:
 + 2n·
+ 2n· 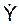 + k2·Y = 0,
+ k2·Y = 0,
где n – коэффициент, характеризующий сопротивление среды и имеющий размерность [рад/с] или [c-1].
В зависимости от соотношения величин n и k материальная точка может совершать или колебательное, или апериодическое (не колебательное) движение.
Дата добавления: 2015-05-30; просмотров: 1675;
