Затухающие колебания материальной точки

Рассмотрим первый вариант движения точки, при котором n < k. В этом варианте общее решение дифференциального уравнения имеет два вида:

Y = (e^-nt)·(C₁·cos(( 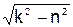)·t) + C₂·sin(( 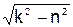)·t));

Y = a·(e^-nt)·sin(( 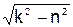)·t + β),

где С₁, С₂, a, β – постоянные интегрирования, определяемые по начальным условиям движения.

Эти выражения называют уравнениями затухающих колебаний материальной точки.

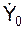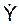Пусть начальными условиями движения являются: t₀ = 0; Y₀; . В этих условиях первый вид решения дифференциального уравнения + 2n· + k²·Y = 0 выражается формулой

Y = (e^-nt)·(Y₀·cos(( 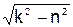)·t) +

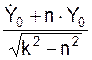+ ·sin(( 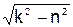)·t)).

Постоянную величину 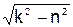называют циклической частотой затухающих колебаний k^*, величину которой определяют по формуле

k^* = .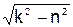

Величина k^* определяет число полных колебаний за промежуток времени, равный 2π = 6,28 с. Тогда имеем

Y = (e^-nt)·(Y₀·cos(k^*·t) + (( 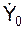+ n·Y₀)/k^*)·sin(k^*·t)).

Как правило, для практических расчётов используют второй вид общего решения дифференциального уравнения движения точки.

Y = a·(e^-nt)·sin(k^*·t + β),

где (k^*·t + β) – фаза затухающих колебаний; β – начальная фаза; a – постоянная интегрирования.

Для определения постоянных интегрирования a и β используют следующую совокупность формул:

а =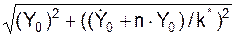

tg(β) = (Y₀·k^*)/( );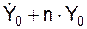

sin(β) = Y₀/ a;

cos(β) = ( 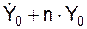)/(а·k^*).

Для характеристики затухающих колебаний используют понятие «период затухающих колебаний Т^*».

Период затухающих колебаний – промежуток времени между двумя последовательными прохождениями точки в одном направлении через положение покоя.

Период затухающих колебаний ( 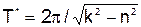= 2π/k^*) больше периода свободных колебаний (T = 2π/k) точки.

На рис. 2.5 приведён общий вид графика затухающих колебаний.

На рис. 2.5 использованы начальные условия движения точки, приведённые на рис. 2.4. График затухающих колебаний располагается в зоне, ограниченной двумя кривыми линиями, описываемыми математическими выражениями: Y = а·e^-nt; Y = – а·e^-nt.

Для характеристики затухающих колебаний используют также понятие «амплитуда а_i затухающих колебаний».

Амплитуда затухающих колебаний – величина наибольшего отклонения точки в ту или другую сторону от положения статического равновесия в течение каждого колебания.

Из рис. 2.5 видно, что амплитуда затухающих колебаний переменна. При этом последующая амплитуда а_i+1 меньше предыдущей амплитуды а_i. Это уменьшение характеризуется отношением

а_i+1/ а_i = e^{– nT*/2} = const.

Число e^{– nT*/2} называют декрементом колебаний; натуральный логарифм этого числа (ln(e^{– nT*/2})), т. е. величину – nT^*/2, называют логарифмическим декрементом.

Зная предыдущее значение а_i амплитуды, последующее значение а_i+1 находят по формуле

а_i+1 = а_i·e^{– nT*/2}.

Следует отметить, что в некоторых учебниках коэффициент n сопротивления среды называют коэффициентом затухания.

Практика показывает, что затухание колебаний происходит очень быстро даже при малом сопротивлении. Так, например, при n = 0,05·k имеем Т^*= 1,00125·Т, e^–nT* = 0,7301, т. е. период Т^* затухающих колебаний отличается от периода Т свободных колебаний лишь на 0,125 %, а амплитуда а_i за время одного полного колебания уменьшается на 0,27 своей величины, и после 10 полных колебаний становится равной 0,043 своего первоначального значения.

Таким образом, основное влияние сопротивления на свободные колебания материальной точки выражается в уменьшении амплитуды колебаний с течением времени, т. е. в затухании колебаний.

Затухающие колебания называют также колебаниями с малым сопротивлением внешней среды.