Колебания материальной точки. Рассмотрим движение материальной точки на гладкой горизонтальной поверхности
 |
Рассмотрим движение материальной точки на гладкой горизонтальной поверхности, происходящее под действием постоянной системы сил, восстанавливающей силы, силы сопротивления движению, пропорциональной первой степени скорости, и возмущающей силы, изменяющейся по периодическому закону (рис. 2.15).
Начало системы отсчёта ОY поместим в положение статического равновесия материальной точки, при котором пружина не деформирована.
Основное уравнение динамики точки для рассматриваемого случая имеет вид
m·a = ΣFiE + ΣRiE = G+ Q+ Rc + N+ Fyn.
Необходимо отметить, что силы G, Q являются активными силами, а силы Rc, N, Fyn отнесены к разряду реакций связей. Так как силы G и N не влияют на горизонтальное движение точки, то они на рис. 2.15 не показаны.
Из предыдущего материала, изложенного в данном разделе учебно-методического пособия, известно:
Rc = – α·V; Fyn = c·Δ; Q = H·sin(p·t + δ).
С учётом этого дифференциальное уравнение горизонтального движения точки описывается равенством
m·  = Σ
= Σ 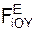 + Σ
+ Σ 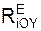 = H·sin(p·t + δ) – α·
= H·sin(p·t + δ) – α· 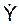 – c·Y.
– c·Y.
Перенеся члены α· 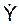 , c·Y в левую часть равенства и разделив обе его части на массу m, получим
, c·Y в левую часть равенства и разделив обе его части на массу m, получим
 + (α/m)·
+ (α/m)· 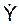 + (c/m)·Y = (H/m)·sin(p·t + δ),
+ (c/m)·Y = (H/m)·sin(p·t + δ),
где c/m = k2 – квадрат циклической частоты свободных колебаний; α/2m = n – коэффициент затухания; H/m = h – отношение амплитуды возмущающей силы к массе точки.
При этих обозначениях дифференциальное уравнение движения точки имеет вид
 + 2n·
+ 2n· 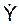 + k2·Y = h·sin(p·t + δ).
+ k2·Y = h·sin(p·t + δ).
Последнее уравнение представляет собой дифференциальное уравнение вынужденных колебаний точки при наличии сопротивления движению, пропорционального скорости.
Общее решение этого уравнения состоит из общего решения Y* дифференциального уравнения  + 2n·
+ 2n· 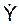 + k2·Y = 0 и частного решения Y**.
+ k2·Y = 0 и частного решения Y**.
Таким образом, общее решение дифференциального уравнения  + 2n·
+ 2n· 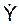 + k2·Y = h·sin(p·t + δ) имеет вид Y = Y*+ Y**.
+ k2·Y = h·sin(p·t + δ) имеет вид Y = Y*+ Y**.
Частное решение Y** выражается формулой
Y** = Ac·sin(p·t + δ – ε),
где Ас, ε – постоянные величины, не зависящие от начальных условий движения точки.
Эти постоянные называют: Ас – амплитуда вынужденных колебаний при наличии сопротивления движению; ε – сдвиг фазы.
Значения Ас и ε определяют по следующей совокупности формул:
Ac = h/( 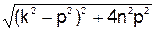 ); tg(ε) = 2·n·p/(k2 – p2);
); tg(ε) = 2·n·p/(k2 – p2);
sin(ε) = 2·n·p·Ac/h; cos(ε) = Ac·(k2 – p2)/h.
Общее решение дифференциального уравнения  + 2n·
+ 2n· 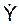 + k2·Y = h·sin(p·t + δ)) в зависимости от соотношения величин k и n имеет вид:
+ k2·Y = h·sin(p·t + δ)) в зависимости от соотношения величин k и n имеет вид:
при n < k Y = a·(e-nt)·sin(k*·t + β) + Ac·sin(p·t + δ – ε);
при n = k Y = (e-nt)·(C1·t + C2) + Ac·sin(p·t + δ – ε);
при n > k Y = (e-nt)·(C1· 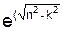 )·t + C2·
)·t + C2· 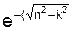 )·t) +
)·t) +
+ Ac·sin(p·t + δ – ε),
где α, β, С1, С2 – постоянные интегрирования, определяемые по начальным условиям движения точки.
 |
На рис. 2.16 приведены графики зависимостей: Y* = f1(t); Y** = f2(t); Y = f3(t) для случая, когда n < k; p > k, и начальных условий Y0 > 0,
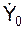 > 0.
> 0.
 |
На рис. 2.17 приведены графики зависимостей Y* = f1(t), Y** = f2(t), Y = f3(t) для случая, когда n = k; p > k, и начальных условий Y0 > 0;
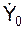 >0.
>0.
Таким образом, графики зависимостей Y = f3(t) на рис. 2.16, 2.17 при p > k представляют собой наложение высокочастотных вынужденных колебаний Y** = f2(t) соответственно на затухающие колебания (см. рис. 2.16) или апериодическое движение (см. рис. 2.17).
Дата добавления: 2015-05-30; просмотров: 981;
