Материальной точки

Алгоритм решения задач динамики несвободной материальной точки при её колебательном движении содержит следующие действия.

1. В механической системе выделяют материальную точку, движение которой рассматривают.

2. Выбирают инерциальную систему отсчёта, начало которой помещают в положение статического равновесия материальной точки.

3. В выбранной системе отсчёта точку изображают в произвольный момент времени таким образом, чтобы она имела положительную координату и двигалась в сторону её увеличения ускоренно.

4. По исходным данным задачи определяют и изображают на рисунке начальные условия движения: Y₀; .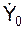

5. К точке прикладывают активные (задаваемые) силы F_i^E.

6. Согласно аксиоме связей эти связи отбрасывают и действие их заменяют соответствующими реакциями R_i^E связей.

ПРИМЕЧАНИЕ.

Если точка движется не по горизонтали, то рассматривают равновесие материальной точки. Из условия равновесия (ΣF_i^E + ΣR_i^E = 0) определяют деформацию пружины при действии на неё постоянной системы активных сил F_i^Е.

7. Записывают дифференциальные уравнения движения точки, приводят их к стандартному виду и записывают решения:

а) + k²·Y = 0; Y = A·sin(k·t + β) – свободные колебания;

б) + 2n· 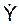+ k²·Y = 0;

если n < k, то Y = a·(e^-nt)·sin(k^*·t + β) – затухающие колебания;

если n = k, то Y = (e^-nt)·(C₁·t + C₂) – апериодическое движение;

если n > k, то Y = (e^-nt)·(C₁· 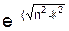^)·t + C₂· 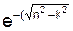^)·t) –

– апериодическое движение;

в) + k²·Y = h·sin(p·t + δ);

если р < k, то Y = A·sin(k·t + β) + (h/(k² – p²))·sin(p·t + δ);

если р > k, то Y = A·sin(k·t + β) + (h/(р² – k²))·sin(p·t + δ – π) –

– вынужденные колебания соответственно малой и

большой частоты под действием

восстанавливающей и возмущающей сил;

г) + 2n· 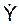+ k²·Y = h·sin(p·t + δ);

если n < k, то Y = a ·(e^-nt)·sin(k^*·t + β) + A_c·sin(p·t + δ – ε);

если n = k, то Y = (e^-nt)·(C₁·t + C₂) + A_c·sin(p·t + δ – ε);

если n > k, то

Y = (e^-nt)·(C₁· 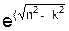^)·t + C₂· 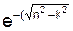^)·t) + A_c·sin(p·t + δ –ε).

8. По начальным условиям движения точки определяют постоянные интегрирования по формулам, приведённым в разделе 2 данного учебно-методического пособия.

9. Полученное решение Y = f(t) иллюстрируется соответствующими графиками.