Случай 1.
Переносное движение – неравномерное вращение тела вокруг неподвижной оси, относительное движение – прямолинейное (рис. 3.4).
В этом случае переносное ускорение ae равно геометрической сумме центростремительного и вращательного ускорений:
ae = 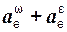 ,
,
где 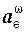 ,
, 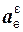 – соответственно центростремительное и вращательное переносные ускорения.
– соответственно центростремительное и вращательное переносные ускорения.
В соответствии с этим имеем
Фе = – m·ae = – m·( 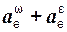 ) = – m·
) = – m· 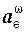 – m·
– m· 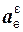 =
= 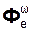 +
+ 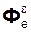 ,
,
где 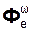 = – m·
= – m· 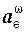 – центробежная переносная сила инерции;
– центробежная переносная сила инерции; 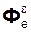 = – m·
= – m· 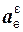 – вращательная переносная сила инерции.
– вращательная переносная сила инерции.
Для рассматриваемого случая модули переносных центробежной и вращательной сил инерции находят по формулам:

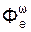 = m·(ωe)2·Х;
= m·(ωe)2·Х;
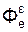 = m·εе·Х,
= m·εе·Х,

где ωе = I 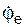 I, εе = I
I, εе = I 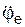 I – соответственно модули угловой скорости и углового ускорения переносного вращения.
I – соответственно модули угловой скорости и углового ускорения переносного вращения.
Основное уравнение динамики и дифференциальные уравнения относительного движения точки в этом случае описываются следующими выражениями:
m·ar = ΣFiЕ + ΣRiЕ + 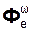 +
+ 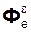 + Фс;
+ Фс;
m· 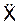 = Σ
= Σ  + Σ
+ Σ  +
+ 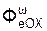 +
+ 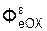 +
+ 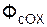 ;
;
m·  = Σ
= Σ  + Σ
+ Σ  +
+ 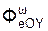 +
+ 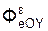 +
+ 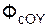 ;
;
m· 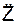 = Σ
= Σ  + Σ
+ Σ  +
+ 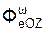 +
+ 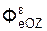 +
+ 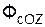 .
.
Дата добавления: 2015-05-30; просмотров: 1541;
