Двумерная случайная величина.
Двумерной случайной величиной называется упорядоченная пара случайных величин 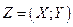 .
.
Каждое значение двумерной случайной величины Z это упорядоченная пара чисел x и y. Вероятность этого значения это вероятность совместного наступления событий:
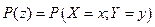
Пусть двумерная случайная величина Z принимает только дискретные значения, т.е. обе случайные величины x и y являются дискретными. Тогда каждое значение случайной величины Z определяется парой 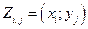 и характеризуется совместной вероятностью
и характеризуется совместной вероятностью 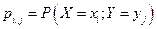 .
.
Закон распределения дискретной двумерной величины можно записать в виде таблицы, которая называется корреляционной таблицей и содержит значения случайных величин X и Y и их совместные вероятности.
таблица 1.
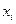
| 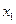
| 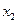
| ... | 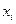
| ... | ||
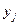
| |||||||
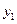
| 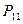
| 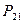
| 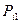
| 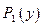
| |||
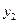
| 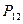
| 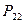
| 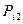
| 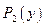
| |||
| ... | |||||||
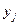
| 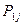
| 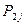
| 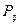
| 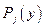
| |||
| ... | |||||||
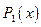
| 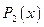
| 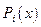
| 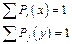
|
В нижней строчке таблицы стоят полные вероятности для каждого из значений Х.
(1) 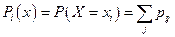
В крайнем правом столбце таблицы стоят полные вероятности для каждого из значений Y.
(2) 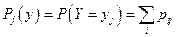
Из каждой из составленной случайной величины можно составить отдельный закон распределения.
таблица 2.
| 
| ... | 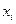
|
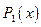
| 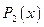
| 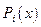
|
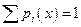
таблица 3.
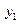
| 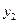
| ... | 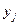
|
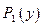
| 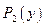
| 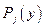
|
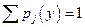
Для случайных величин X и Y по таблице 2 и 3 можно вычислить M и D по обычным формулам.
Пример № 1.
Пусть двумерная случайная величина Z (X; Y) задана корреляционной таблицей. Найти:
1) вероятность того, что P (Z), где Z (10;200)
2) M(X), D(X), σ(X)
M(Y), D(Y), σ(Y)
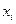
| 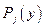
| ||||
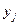
| |||||
| 0,1 | 0,2 | 0,1 | 0,4 | ||
| 0,3 | 0,1 | 0,2 | 0,6 | ||
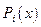
| 0,4 | 0,3 | 0,3 | 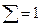
|
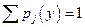
1) Р (10;200)=0,3
2)
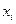
| |||
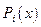
| 0,4 | 0,3 | 0,5 |
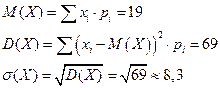
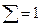
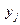
| ||
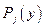
| 0,4 | 0,6 |
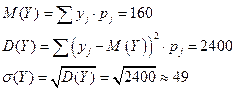
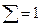
Для двумерной случайной величины вводят понятие условного распределения. Фиксируем какое-либо значение одной из случайных величин и находим условную вероятность для другой случайной величины.
(3) 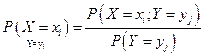 , где
, где
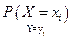 - условная вероятность того, что
- условная вероятность того, что 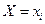 при условии, что Y принимает значения i и j;
при условии, что Y принимает значения i и j;
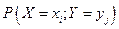 - совместная вероятность того, что
- совместная вероятность того, что 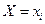 ,
, 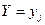 , т.е.
, т.е. 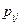
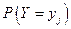 - полная вероятность того, что Y приняло значение
- полная вероятность того, что Y приняло значение 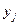 , т.е.
, т.е. 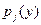
(3) 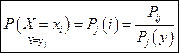
Аналогично можно определить условную вероятность того, что Y принимает значение 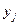 при фиксированном значении Х.
при фиксированном значении Х.
(4) 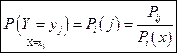
Пример № 1 (продолжение):
1) вычислить условную вероятность, что х = 30 при y = 100;
2) составить условное распределение для х при y = 200;
3) найти условную вероятность, что y = 100 при х = 20;
4) составить условное распределение для y при х = 10;
1) 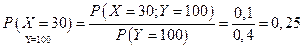
2) y = 200
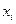
| |||
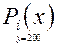
| 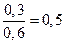
| 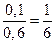
| 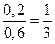
|
3) 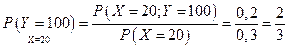
4) x = 10
| ||
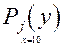
| 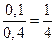
| 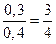
|
Дата добавления: 2015-05-26; просмотров: 1214;
