Линейная регрессия.

Если уравнение регрессии является линейным, то говорят, что между x и y существует линейная корреляционная зависимость.

Линейная корреляционная зависимость задается следующими уравнениями зависимости:

(I) 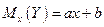- I линейное уравнение регрессии y по х;

(II) 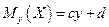- II линейное уравнение регрессии х по y;

Как правило параметры a, b, c, d неизвестны.

Чтобы их найти организуют случайную выборку и по результатам этой выборки методом наименьших квадратов определяют параметры a, b, c, d.

Мерой тесноты линейной корреляционной зависимости является коэффициент линейной корреляции.

(9)

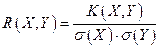
По результатам выборки неизвестные характеристики генеральной совокупности заменяются их выборочными оценками.

Генеральная совокупность	Выборочная оценка	Генеральная совокупность	Выборочная оценка

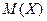
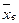
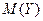
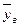
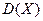
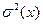
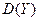
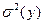
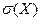
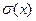
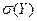
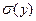
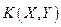
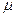
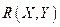
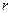
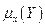
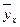
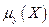
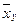
μ – выборочный корреляционный момент

(10)

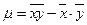
(11) 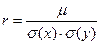-выборочный коэффициент линейной корреляции;

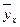- групповые средние y по x, т.е. средние значения y вычисленные при фиксированном значении x;

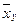- групповые средние x по y, т.е. средние значения x вычисленные при фиксированном значении y;