Нахождение параметров линейных уравнений регрессии методом наименьших квадратов.
После того, как сделана выборка, в линейных уравнениях регрессии I и II условные математические ожидания заменяются их оценками – групповыми средними. Тогда уравнения регрессии принимают следующий вид:
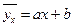 - I
- I
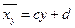 - II
- II
Метод наименьших квадратов состоит в том, что неизвестные параметры a и b – I, c, d – II находятся из принципа минимизации суммы квадратов расстояний от опытных точек, полученных по выборке, до теоретических точек, полученных соответственно по уравнениям I и II.
Для нахождения min указанной суммы, находятся частный производные и приравниваются к 0. Получается сумма уравнений, которые называются нормальными системами:
I 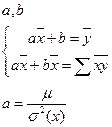
Коэффициент а в уравнении регрессии I называют коэффициентом регрессии y по x и обозначается:
(12) 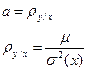
Тогда уравнение регрессии I приобретает вид:
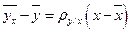 - I
- I
В дальнейшем для удобства 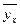 обозначается y и уравнение I приобретает вид:
обозначается y и уравнение I приобретает вид:
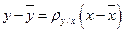 - I, где
- I, где
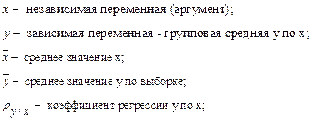
IIаналогично с помощью M и K составляем систему нормальных уравнений для нахождения параметров c и d.
Коэффициент с обозначением 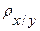 называется коэффициентом регрессии x по y.
называется коэффициентом регрессии x по y.
(13) 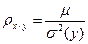
Тогда уравнение регрессии II приобретает вид:
 - II
- II
В дальнейшем для удобства 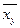 обозначается y и уравнение II приобретает вид:
обозначается y и уравнение II приобретает вид:
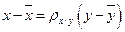 - II, где
- II, где
Дата добавления: 2015-05-26; просмотров: 658;
