ЛИНЕЙНАЯ ОБОЛОЧКА СИСТЕМЫ ВЕКТОРОВ

Пусть векторы e₁, e₂, … e_nÎV и a₁,a₂, … a_nÎK.

Вектор x = a₁e₁ + a₂e₂ + … + a_ne_n = 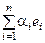называется линейной комбинацией векторов e₁, e₂, … , e_n с коэффициентами a₁,a₂, … a_n.

Если все коэффициенты в линейной комбинации равны нулю, то линейная комбинация называетсятривиальной.

Множество всевозможных линейных комбинаций векторов называется линейной оболочкой этой системы векторов и обозначается:

ℒ(e₁, e₂, …, e_n) = ℒ .

8°. ℒ(e₁, e₂, …, e_n) является линейным пространством.

◀ Корректность операций сложения и умножения на скаляр следует из того, что ℒ(e₁, e₂, …, e_n) – это множество всевозможных линейных комбинаций. Нейтральный элемент – это тривиальная линейная комбинация. Для элемента х = 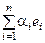противоположным является элемент –x = 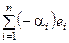. Аксиомы, которым должны удовлетворять операции, также выполнены. Таким образом, ℒ(e₁, e₂, …, e_n) является линейным пространством.

Любое линейное пространство содержит в себе в, общем случае, бесконечное множество других линейных пространств (подпространств) – линейных оболочек ▶

В дальнейшем мы постараемся ответить на следующие вопросы:

Когда линейные оболочки разных систем векторов состоят из одних и тех же векторов (т.е. совпадают)?

2) Какое минимальное число векторов определяет одну и ту же линейную оболочку?

3) Является ли исходное пространство линейной оболочкой некоторой системы векторов?