ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ

Система векторов {e₁, e₂, …, e_n} называется линейно независимой, если 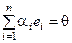тогда и только тогда, когда a₁=a₂ =… = a_n = 0.

Если, при 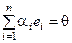, хотя бы один из коэффициентов не равен нулю, то система векторов называется линейно зависимой.

Можно выделить следующие свойства линейно зависимых систем векторов:

11°. Система, состоящая из одного вектора x, линейно зависима тогда и только тогда, когда x = q.

◀ а) Система линейно зависима Þ $a ¹ 0 | a⊙x = q Þ x = q (т. 6°);

б) x = q. Возьмем a = 1 Þ ax = aq = q (т. 5°). ▶

12°. Набор векторов {e₁, e₂, …, e_k,q} содержащий q, линейно зависим.

◀ 0⊙e₁, 0⊙e₂, …, 0⊙e_n + 1⊙q = q. Так как записанная линейная комбинация содержит коэффициент не равный нулю, то система линейно зависима. ▶

13°. Если хотя бы один вектор из системы выражается как линейная комбинация других, то система векторов линейно зависима (и наоборот).

◀ Пусть есть система векторов e₁, e₂,…, e_n–1, e_n и пусть e_n = a₁e₁+ a₂e₂ + … + a_{n –1}e_{n –1}. Тогда либо e_n = q и система линейно зависима, либо e_n ¹ q и тогда набор a₁,a₂, … a_n–1нетривиален, т.е. 1⊙ e_n– a₁e₁– a₂e₂ –…– a_n–1e_n–1= q при нетривиальном наборе коэффициен-

тов. Следовательно, система линейно зависима.▶

14°. Если система векторов линейно зависима, то, по крайней мере, один из векторов может быть представлен как линейная комбинация остальных.

◀ Так как система векторов линейно независима, то существует нетривиальный набор a₁, a₂, …, a_n такой, что a₁e₁+ a₂e₂ +…+ a_ne_n = q. Пусть a_n ¹ 0. Тогда . ▶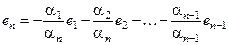

15°. Любая часть линейно независимого набора векторов линейно независима.

◀ Пусть e₁, e₂, … , e_k, e_{k + 1}, …, e_n линейно независима. Рассмотрим равенство a₁e₁ + a₂e₂ + …+ a_ke_k + a_{k +1} + e_{k +1} +… + a_ne_n= q. В силу линейной независимости оно выполнено тогда и только тогда, когда a₁₌ a₂₌ …= a_n = 0. Положив a_{k +1}, a_{k +2}, …, a_n равными 0 получим: a₁e₁+ a₂e₂ +…+ a_ke_k = = q Þ a₁= a₂= …= a_k = 0.Т.е. система e₁, e₂, … , e_k линейно независима.▶

Если пространство V не есть {q}, то в нем есть, по меньшей мере, один ненулевой вектор. Т.е. если V ¹ {q}, то в нем существует линейно независимая система векторов.

Используя процесс «посадки» (добавления в линейно независимую систему векторов, других векторов пространства, не нарушающих свойство линейной независимости) можно построить в пространстве максимальный линейно независимый в V набор векторов.