Здесьпредполагается, что дискретная случайная величина имеет изначений. Выражение (2.9) называется условием нормировки.
Случайной величиной является число очков, выпадающих на верхней грани игральной кости. Указать распределение этой случайной величины (табл. 2).
Таблица 2
| X | ||||||
| р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Случайной величиной является номер вида спорта в игре «Спортло-10». Общее число видов равно 49. Указать распределение этой случайной величины (табл. 3).
Таблица 3
| X | … | ||||
| р | 1/49 | 1/49 | 1/6 | … | 1/49 |
Биномиальное распределение.Пусть некоторое испытание проводится трижды и при этом событие А происходит I раз (I — случайная величина, которая при тройном испытании может принимать значения 0, 1, 2 и 3). Вероятность наступления события А равна Р(А); вероятность того, что событие А не происходит, т. е. имеет место противоположное событие А, равна [1 - Р(А)].
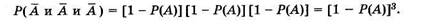 |
Значение 1 = 0 соответствует такому случаю, при котором трижды подряд событие А не происходило. Вероятность этого сложного события, по теореме умножения вероятностей (2.6), равна
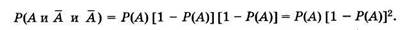 |
Значение I = 1 относится к случаю, при котором событие А произошло в одном из трех испытаний. По формуле (2.6) получаем
Так как при l = 1 происходят также и два других сложных события: (А и А и А)и(А и А и А), то необходимо, воспользовавшись теоремой сложения вероятностей (2.4), получить полную вероятность для l = 1, сложив трижды предыдущее выражение:
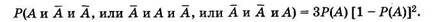
Значение I = 2 соответствует случаю, при котором событие А произошло в двух из трех испытаний. Рассуждениями, подобными приведенным выше, получим полную вероятность для этого случая:
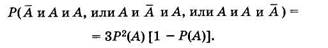
При 1 = 3 событие А появляется во всех трех испытаниях. Используя теорему умножения вероятностей, находим
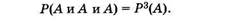
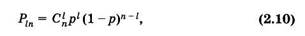 |
В общем случае биномиальное распределение позволяет определить вероятность того, что событие А произойдет l раз при п испытаниях:
На основе многолетних наблюдений вызов врача в данный дом оценивается вероятностью 0,5. Найти вероятность того, что в течение шести дней произойдет четыре вызова врача; Р(А) = 0,5, п = 6,1 = 4. Т Воспользуемся формулой (2.10):
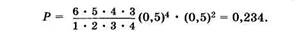
Числовые характеристики дискретной случайной величины.Во многих случаях, наряду с распределением случайной величины или вместо него, информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины. Рассмотрим наиболее употребительные из них.
Математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значе
ний на вероятности этих значений:
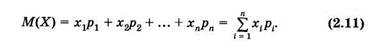
Пусть при большом числе испытаний п дискретная случайная величина X принимает значения xv x2, ..., хп соответственно m1 , mг, ..., тп раз. Среднее значение равно
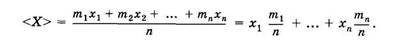
Если п велико, то относительные частоты т1/п, т2/п, ... будут стремиться к вероятностям, а средняя величина — к математическому ожиданию. Именно поэтому математическое ожидание часто отождествляют со средним значением.
Найти математическое ожидание для дискретной случайной величины, которая задается цифрой на грани при бросании игральной кости (см. табл. 2).
Используем формулу (2.11):
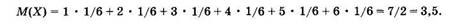
Найти математическое ожидание для дискретной случайной величины, которая определяется тиражом «Спортлото» (см. табл. 3). Согласно формуле (2.11), находим
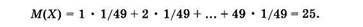 |
Возможные значения дискретной случайной величины рассеяны вокруг ее математического ожидания, часть из них превышает М{Х), часть — меньше М{Х). Как оценить степень разброса случайной величины относительно ее среднего значения? Может показаться, что для решения такой задачи следует вычислить отклонения всех случайных величин от ее математического ожидания X - М(Х), а затем найти математическое ожидание (среднее значение) этих отклонений: М[Х - М(Х)]. Вез доказательства отметим, что эта величина равна нулю, так как отклонения случайных величин от математического ожидания имеют как положительные, так и отрицательные значения. Поэтому целесообразно учитывать либо абсолютные значения отклонений М[Х — М (X)], либо их квадраты М[Х - М(Х)]2. Второй вариант оказывается предпочтительнее, так приходят к понятию дисперсии случайной величины.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
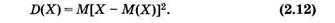 |
Без вывода приведем удобную для вычисления дисперсии формулу
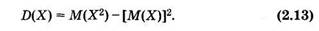 |
Она означает, что дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания.
Найти дисперсию случайной величины, которая задается цифрой на грани при бросании игральной кости (см. табл. 2).
Математическое ожидание этого распределения равно 3,5. Запишем значения квадратов отклонения случайных величин от математического ожидания: (1 - 3,5)2 = 6,25; (2 - 3,5)2 = 2,25; (3 - 3,5)2 = 0,25; (4 - 3,5)2 = 0,25; (5 - 3,5)2 = 2,25; (6 - 3,5)2 = 6,25. По формуле (2.12) с учетом (2.11) няходим дисперсию:
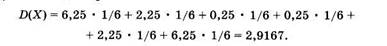
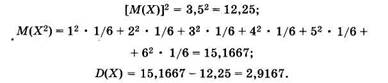
Как следует из (2.12), дисперсия имеет размерность квадрата размерности случайной величины. Для того чтобы оценивать расстояние случайной величины в единицах той же размерности, вводят понятие среднего квадратического отклонения, под которым понимают квадратный корень из дисперсии:

Распределение и характеристики непрерывной случайной величины. Непрерывную случайную величину нельзя задать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.
Пусть dP — вероятность того, что непрерывная случайная величина X принимает значения между х и х + dx. Очевидно, что Ирм больше интервал dx, тем больше и вероятность dP: dP ~ dx. Шроме того, вероятность должна зависеть и от самой случайной Величины, вблизи которой расположен интервал, поэтому

где f(x) — плотность вероятности, или функция распределения вероятностей. Она показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой этой величины:

Интегрируя выражение (2.15) в соответствующих пределах, находим вероятность того, что случайная величина принимает какое-либо значение в интервале (ab):

Условие нормировки для непрерывной случайной величины имеет вид

Как видно из (2.19), эта функция равна вероятности того, что случайная величина принимает значения, меньшие х:

Для непрерывной случайной величины математическое ожидание и дисперсия записываются соответственно в виде
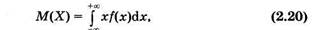
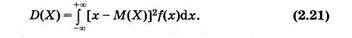
Дата добавления: 2015-06-22; просмотров: 1365;
