Случай 2.
Переносное движение – равномерное вращение ( 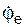 = const) вокруг неподвижной оси, относительное движение – прямолинейное (рис. 3.5).
= const) вокруг неподвижной оси, относительное движение – прямолинейное (рис. 3.5).
В этом случае угловое ускорение переносного вращения 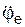 = 0 и, следовательно, переносная вращательная сила инерции
= 0 и, следовательно, переносная вращательная сила инерции 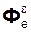 = 0.
= 0.
 |
Тогда основное уравнение динамики и дифференциальные уравнения относительного движения точки описываются выражениями:
m·ar = ΣFiЕ + ΣRiЕ + 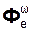 + Фс;
+ Фс;
m· 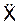 = Σ
= Σ  + Σ
+ Σ  +
+ 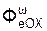 +
+ 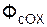 ;
;
m·  = Σ
= Σ  + Σ
+ Σ  +
+ 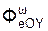 +
+ 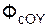 ;
;
m· 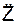 = Σ
= Σ  + Σ
+ Σ  +
+ 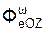 +
+ 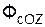 .
.
Случай 3.
Переносное движение – поступательное неравномерное криволинейное движение, относительное движение – прямолинейное (рис. 3.6).

Согласно рис. 3.6 механизм содержит кривошипы 1, 2 и прямоугольную пластину 3, по которой перемещается материальная точка по закону Х = f(t). При этом О1А = О2В. Кривошипы 1, 2 совершают вращательные движения с угловыми скоростями  ,
,  . Пластина 3 совершает поступательное движение. Так как О1А = О2В, то φ1 = φ2,
. Пластина 3 совершает поступательное движение. Так как О1А = О2В, то φ1 = φ2,  =
=  ,
, 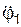 =
= 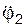 .
.
Исходя из этого, имеем: ω3 = ωе = 0 = const; ε3 = εe = 0, где ω3 – модуль угловой скорости тела 3; ωе – модуль угловой скорости переносного вращения.
Поскольку кориолисова сила Фс = 0, то основное уравнение динамики относительного движения принимает вид
m·ar = ΣFiЕ + ΣRiЕ + Фе,
где Фе = – m·ae – переносная сила инерции.
Так как переносное движение является поступательным, то его ускорение ae равно ускорению точки А тела 3. С другой стороны, точка А принадлежит кривошипу О1А, совершающему вращательное неравномерное движение (ω1 ≠ 0; ε1 ≠ 0). Тогда
ae = aА = 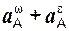 =
= 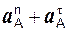 =
= 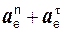 ,
,
где 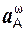 ,
, 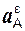 – соответственно центростремительное и вращательное ускорения точки А кривошипа О1А;
– соответственно центростремительное и вращательное ускорения точки А кривошипа О1А; 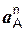 ,
, 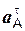 – нормальное и касательное ускорения точки А тела 3;
– нормальное и касательное ускорения точки А тела 3; 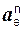 ,
,  – соответственно нормальное и касательное переносные ускорения.
– соответственно нормальное и касательное переносные ускорения.
Отсюда вытекает очевидные равенства:
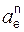 =
= 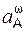 = (ω1)2·r;
= (ω1)2·r;  =
=  = ε1·r;
= ε1·r;
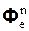 = – m·
= – m· 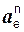 ;
; 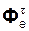 = – m·
= – m·  ,
,
где 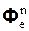 ,
, 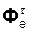 – переносные нормальная и касательная силы инерции.
– переносные нормальная и касательная силы инерции.
С учетом того, что Фе = 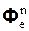 +
+ 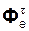 , имеем:
, имеем:
m·ar = ΣFiЕ + ΣRiЕ + 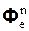 +
+ 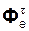 ;
;
m· 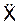 = Σ
= Σ  + Σ
+ Σ  +
+ 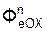 +
+  ;
;
m·  = Σ
= Σ  + Σ
+ Σ  +
+ 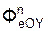 +
+ 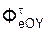 ;
;
m· 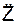 = Σ
= Σ  + Σ
+ Σ  +
+ 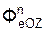 +
+ 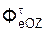 .
.
Дата добавления: 2015-05-30; просмотров: 1307;
