Переносная и кориолисова силы инерции
Два первых закона классической механики и полученные на их основе уравнения справедливы при движении точки в инерциальной системе отсчёта (ИСО). Существует ряд технических задач, в которых рассматривают движение материальной точки в подвижной системе отсчёта (ПСО), которая в общем случае не является инерциальной.
Инерциальная система отсчёта – система отсчёта, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.
Система отсчёта, не обладающая этим свойством, называется неинерциальной системой отсчёта
Рассмотрим движение материальной точки под действием активных сил FiЕ и реакций RiЕ относительно подвижной неинерциальной системы отсчёта OXYZ (рис. 3.1).
Напомним некоторые понятия кинематики, используемые в данном разделе динамики точки.
Движение точки по отношению к неподвижной системе отсчёта O1X1Y1Z1 называется абсолютным и характеризуется абсолютной скоростьюV и абсолютным ускорениемa. Положение точки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравнениями абсолютного движения:
X1 = f1(t); Y1 = f2(t); Z1 = f3(t).
Неподвижная система отсчёта O1X1Y1Z1 является инерциальной. В этой системе отсчёта основное уравнение динамики имеет вид
m·a = ΣFiЕ + ΣRiЕ,
где FiЕ – активная сила; RiЕ – реакция внешней связи.
 |
Движение точки по отношению к подвижной системе отсчёта OXYZ называется относительным и характеризуется относительной скоростью Vr и относительным ускорением ar. Положение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые называются уравнениями относительного движения:
X = f4(t); Y = f5(t); Z = f6(t).
Подвижная система отсчёта OXYZ не является инерциальной. Применение в чистом виде первого и второго законов классической механики в ПСО неправомерно.
Рассмотрим переносное движение точки (рис. 3.2) и напомним суть некоторых понятий кинематики, используемых в этом разделе динамики.
Если координаты точки в ПСО постоянны (Х = C1 = const; Y = C2 = const; Z = C3 = const), то движение этой точки вместе с ПСО по отношению к неподвижной системе отсчёта называют переносным движением. Это движение характеризуется переносной скоростьюVe и переносным ускорениемae. Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями переносного движения:
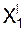 = f7(t)
= f7(t) 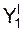 = f8(t)
= f8(t) 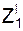 = f9(t).
= f9(t).
 |
Из курса кинематики известно, что абсолютное ускорение a точки определяют по формуле
a = ar + ae + ac,
где ar – относительное ускорение; ae – переносное ускорение; ac – ускорение Кориолиса.
Ускорение Кориолиса определяют по формуле
ac = 2( 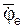 × Vr),
× Vr),
где 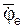 – вектор угловой скорости переносного вращения.
– вектор угловой скорости переносного вращения.
Модуль кориолисова ускорения находят по формуле
ac = 2ωe·Vr·sin( 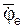 ,Vr),
,Vr),
где ωе = I 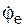 I – модуль угловой скорости
I – модуль угловой скорости 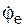 переносного вращения.
переносного вращения.
Кориолисово ускорение равно нулю в трех случаях:
1) если ωe = 0, т. е. в случае поступательного переносного движения или в момент обращения в нуль угловой скорости 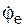 непоступательного переносного движения;
непоступательного переносного движения;
2) если Vr = 0, т. е. в случае относительного покоя точки или в момент равенства нулю относительной скорости движущейся точки;
3) если sin( 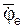 ,Vr) = 0, т. е. в случае, когда вектор относительной скорости Vr и вектор переносной угловой скорости
,Vr) = 0, т. е. в случае, когда вектор относительной скорости Vr и вектор переносной угловой скорости 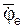 параллельны.
параллельны.
Направление кориолисова ускорения определяется по правилу векторного произведения. Согласно этому правилу вектор ac одновременно перпендикулярен векторам 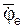 и Vr. При этом ac направлено в сторону, откуда поворот вектора
и Vr. При этом ac направлено в сторону, откуда поворот вектора 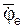 к вектору Vr для совмещения их направлений виден происходящим против хода часовой стрелки. Поворот осуществляется на угол меньше 180о.
к вектору Vr для совмещения их направлений виден происходящим против хода часовой стрелки. Поворот осуществляется на угол меньше 180о.
Направление ускорения Кориолиса находят также по правилу Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость Vr точки спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию в той же плоскости на угол 90о в сторону переносного вращения.
Если подставим абсолютное ускорение a = ar + ae + ac в основное уравнение динамики точки m·a = ΣFiЕ + ΣRiЕ, то получим
m·(ar + ae + ac) = ΣFiЕ + ΣRiЕ.
Разрешим это уравнение относительно m·ar:
m·ar = ΣFiЕ + ΣRiЕ – m·ae – m·ac.
Введём два вектора: Фе = – m·ae; Фс = – m·ac. Эти векторы назовем переносной и кориолисовой силами инерции.
При исследовании движения механических систем в теоретической механике используют следующие понятия.
Сила инерции – величина, равная произведению массы материальной точки на её ускорение и направленная противоположно этому ускорению.
Переносная сила инерции при рассмотрении движения материальной точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её переносное ускорение и направленная противоположно этому ускорению.
Кориолисова сила инерции при рассмотрении движения точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её кориолисово ускорение и направленная противоположно этому ускорению.
Используя понятия переносной и кориолисовой сил инерции, получим
m·ar = ΣFiЕ + ΣRiЕ + Фе + Фс.
Последнее выражение называют дифференциальным уравнением относительного движения точки в векторной форме или основным уравнением динамики относительного движения.
Произведение массы m точки на её относительное ускорение ar равно геометрической сумме активных сил FiЕ, реакций внешних связей RiЕ, переносной силы инерции Фе и кориолисовой силы инерции Фс.
Проецируя последнее векторное равенство на координатные оси ПСО, получим дифференциальные уравнения относительного движения точки:
m· 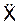 = Σ
= Σ 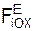 + Σ
+ Σ 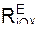 +
+ 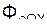 +
+ 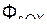 ;
;
m·  = Σ
= Σ  + Σ
+ Σ  +
+ 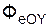 +
+ 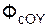 ;
;
m· 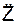 = Σ
= Σ  + Σ
+ Σ  +
+ 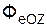 +
+ 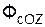 .
.
Произведение массы точки на проекцию её относительного ускорения на координатную ось ПСО равно сумме проекций активных сил, реакций внешних связей и переносной и кориолисовой сил инерции на ту же ось.

Силы инерции Фе, Фс направлены противоположно ускорениям ae, ac (рис. 3.3).
Дифференциальные уравнения относительного движения точки
m· 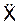 = Σ
= Σ  + Σ
+ Σ  +
+ 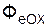 +
+ 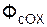 ;
;
m·  = Σ
= Σ  + Σ
+ Σ  +
+ 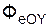 +
+ 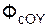 ;
;
m· 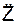 = Σ
= Σ  + Σ
+ Σ  +
+ 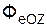 +
+ 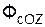
отличаются от дифференциальных уравнений движения точки в инерциальной системе отсчёта (см. раздел 1)
m· 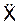 = Σ
= Σ  + Σ
+ Σ  ;
;
m·  = Σ
= Σ  + Σ
+ Σ  ;
;
m· 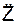 = Σ
= Σ  + Σ
+ Σ 
наличием в правой части этих уравнений проекций на соответствующие координатные оси переносной и кориолисовой сил инерции.
Дата добавления: 2015-05-30; просмотров: 19624;
