Закон инерции квадратичных форм

Следующую теорему называют законом инерции квадратичных форм.

6°. Если форма приведена к каноническому виду двумя различными способами, то число по­ложительных и отрицательных канонических коэффициентов одинаково.

◀ Пусть в базисе {е_i} форма 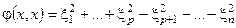и в базисе {f_i} форма 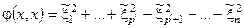и пусть p¢ > p. Из второго соотношения следует, что размерность пространства векторов, на которых форма положительна равна p¢ : dimL⁺ = p¢, а из первого, что dimL^– = n – p. Так, как p¢ + n – p > n следует, что dim(L⁺∩L^–) ¹ 0 т.е. $х ¹ q ½ хÎL⁺ , хÎL^– но тогда 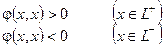. Противоречие. ▶

Количество положительных и отрицательных канонических коэффициентов называется положительным и отрицательным индексом инерции.