Критерий Сильвестра

4°.Для того чтобы форма j(x, x) была положительно определена необходимо и доста­точно, чтобы D_i > 0 ("i = 1, 2, …, n).

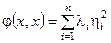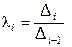◀ Достаточность. Если D_i > 0, то , где т.е. l_i > 0 и тогда форма j(x, x) > 0.

Необходимость: j(x, x) > 0. покажем, что D_k > 0. От противного:

а) Предположим, что D_k > 0, D_i < 0 и нет D_j= 0 по Якоби $l_i тогда j(x, x) < 0 если: 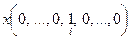, что противоречит положительной определенности квадратичной формы.

б). Пусть D_k = 0, 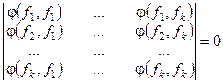, т.е. одна из строк минора есть линейная комбинация остальных:

m₁j(f₁, f_i) + … + m_kj(f_k, f_i) = 0, m_k ¹ 0, i = 1, 2, …, k,

j(m₁f₁ + … + m_k f_k, f_i) = 0 Þ 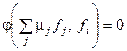"i = 1, 2, …, k Þ

Þ 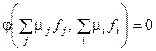Þ j(x, x) = 0, x ¹ 0. Вновь получено противоречие с положительной определенностью формы. ▶

5°. Для того чтобы форма j(x, x) была отрицательно определена необходимо и доста­точно чтобы: D₁ < 0, D₂ > 0, D₃ < 0 … (главные миноры чередуются по знаку, начиная с “–”).

◀ Если форма j(x, x) отрицательно определена, то форма j^­–(x, x) = –j(x, x) положительно определена. Тогда матрицы формы j(x, x) отличаются на множитель (–1)а, следовательно, миноры D_k отличаются на множитель (–1)^k . ▶