Билинейный функционал. Его матрица
Пусть V – линейное вещественное пространство. Если имеется закон, по которому "х, уÎV соответствует некоторое aÎR (числовое поле). Т.е. "х, уÎV ® a = j(х, у)ÎRтакое, что выполняются требования:
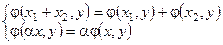 – линейность по 1ому аргументу;
– линейность по 1ому аргументу;
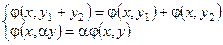 – линейность по 2ому аргументу,
– линейность по 2ому аргументу,
то говорят, что в линейном пространстве V над полем R задан билинейный функционал или билинейная форма j(х, у).
Пусть 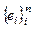 – базис в V. Тогда
– базис в V. Тогда 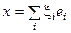 ,
, 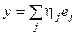 и тогда
и тогда
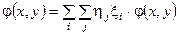 , т.е.
, т.е. 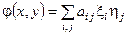 , где аij =j(еi, еj). Матрица
, где аij =j(еi, еj). Матрица 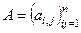 называется матрицей билинейного функционала (или билинейной формы) в базисе
называется матрицей билинейного функционала (или билинейной формы) в базисе 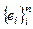 .
.
Билинейный функционал (форма) называется симметричным, если "х, уÎV j(х, у) = j(у, х) и антисимметричным, если "х, уÎV j(х, у) = –j(у, х).
Естественно, что симметричной билинейной форме соответствует симметричная матрица (и наоборот), а антисимметричной билинейной форме соответствует кососимметричная матрица (и наоборот).
1°.Всякая билинейная форма может быть представлена в виде суммы симметрической и антисимметрической билинейных форм. Это представление единственно.
◀ 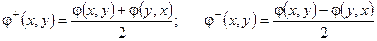 . ▶
. ▶
Дата добавления: 2015-05-05; просмотров: 1197;
