Неоднородные системы

Рассматривается неоднородная система линейных уравнений Ах = b с n-неизвест-ными.

12°. (Кронекер-Капелли). Система Ах = b совместна тогда, и только тогда, когда ранг главной матрицы системы совпадает с рангом расширенной матрицы rangA =rangà (à = (A|b)).

◀ 1) Пусть система Ах = b – совместна Þ $с такой, что Ас = b т.е. c₁S₁ + c₂S₂ +…+ c_nS_n=b. Таким образом, последний столбец матрицы à является линейной комбинацией столбцов матрицы А Þ rangA = rangà .

2). Пусть rangA = Ã . Тогда базисные столбцы общие, т.е. являются столбцами матрицы А Þ столбец b является линейной комбинацией столбцов s_1, s_2, … , s_n Þ$c₁, c_2, …, c_n такие, что c₁S₁ + c₂S₂ +…+ c_nS_n = b т.е. Аc = b. Система совместна.▶

13°. Если неоднородная система линейных уравнений совместна и rangA = rangà = n,то она имеет единственное решение (по теореме Крамера).

Пусть теперь rangA = rangà = r ≤ n.

14°. Разность двух различных решений неоднородной системы линейных уравнений является решением соответствующей однородной системы, т.е. если c⁽²⁾ и c⁽¹⁾ два решения неоднородной системы Ах = b, то c⁽²⁾ – c⁽¹⁾ решением однородной системы Ах = 0.

◀ А(c⁽²⁾ – c⁽¹⁾) = Аc⁽²⁾ – Аc⁽¹⁾ = b – b = 0,т.е. c⁽²⁾ – c⁽¹⁾ = c⁽⁰⁾. Здесь через c⁽⁰⁾ обозначено некоторое решение однородной системы. ▶

15°. Сумма любого решения однородной системы c⁽⁰⁾ и некоторого решения неоднородной системы c⁽¹⁾ есть решение неоднородной системы.

◀ А(c⁽⁰⁾ – c⁽¹⁾) = Аc⁽⁰⁾ + Аc⁽¹⁾ = 0 + b = b.▶

Предыдущие два утверждения доказывают теорему об общем виде решения неоднородной системы и линейных уравнений.

16°. Общее решение неоднородной системы уравнений есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Эту фразу можно записать с помощью легко запоминающейся аббревиатуры:

О. Р. Н. С. = О. Р. О. С. + Ч. Р. Н. С.

Способ решения неоднородных систем линейных уравнений таков:

1). Если rangA = rangà = n, то решение единственно и может быть найдено по Крамеру;

2). ЕслиrangA = rangà = r < n то, записав систему в виде

x₁S₁ + x₂S₂ +…+ x_rS_r = b – x_r+1S_r+1 –…– x_nS_n.

а) положив x_r+1, x_{r+2, …,} x_n равными любим фиксированным значениям, получим систему неоднородную (r- уравнений с r-неизвестными) имеющей единственное решение, ибо ее определитель не равен 0. Тем самым будет найдено частное решение неоднородной системы.

b) выбросив вектор b: x₁S₁ + x₂S₂ +…+ x_rS_r = – x_r+1 S_r+1 –…– x_nS_n и применяя процедуру, описанную в предыдущем параграфе, построим базис в пространстве L решений однородной системы уравнений {e₁, e₂, ..., e_n–r}.

с). Тогда x^{(неодн.)} = x^{(частн.)} +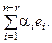

Система векторов {e₁, e₂, ..., e_n–r} называется фундаментальной системой решений для системы уравнений Ах = 0.

Если М – множество решений неоднородной системы уравнений, x^(r)– некоторое частное решение неоднородной системы уравнений, L– пространство решений соответствующей линейной однородной системы, то M = x^(r)+ L, т.е. М – есть линейное многообразие размерности n – r.

§8. Метод Гаусса РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. (метод исключения неизвестных)

Решить систему уравнений: .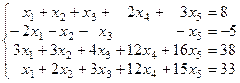

Записав расширенную матрицу системы, преобразуем ее с помощью преобразований не изменяющих ранг матрицы. Цель: в первом столбце все элементы, кроме одного, должны стать равными нулю. Это равносильно тому, что из 2^го, 3^го и 4^го уравнений будет исключена неизвестная х₁. Для достижения цели первую строку, умноженную на 2, –3 и –1 прибавим, соответственно, к 2^ой, 3^ей и 4^ой строке. Получим:

~ .

Примечание: здесь и в дальнейшем знак ~ , стоящий между двумя матрицами означает, что справа и слева от этого знака стоят матрицы одинакового ранга и, следовательно, системы линейных уравнений с такими матрицами имеют одинаковые решения.

Далее вторую строку, умноженную на –1 прибавим к 4^ой строке, тем самым исключив х₂ из третьего и четвертого уравнений и, наконец исключим х₃ из 4^го уравнения, прибавив третью строку, умноженную на –1 к четвертой:

~ ~ .

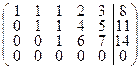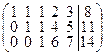Имеем rangA = rangà = 3. Система совместна. n – r =5 –3 = 2, dimL =dimM =2. Так как, размерность пространства решений однородной системы равна 2, то в системе имеется две свободных неизвестных. Выберем в качестве свободных переменных х₃, х₄. Отделим в матрице свободные неизвестные вертикальной пунктирной линией: .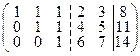

Положив х₄ = 1, х₅ = 1, получим х₁ = х₂ = х₃= 1. Т.е. частное решение неоднородной системы (1, 1, 1, 1, 1).

Далее рассмотрим однородную систему уравнений с матрицей 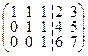. Тогда

.

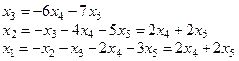Положив х₄ = 1, х₅ = 0 Þ е₁(2, 2, –6, 1, 0). Положив х₄ = 0, х₅ = 1 Þ е₂(2, 2, –7, 0, 1), (е₁, е₂– ба­зис пространства решений). Отсюда х = (1,1,1,1,1) + a(2,2,–6,1,0)+ b(2,2,–7,0,1), где a, b – любые.

Если положить х₄ = х₅ = 0, то получим х₃ = 14, х₂ = –3, х₁ = –3, т.е. (–3, –3, 14, 0, 0) еще одно частное решение данной системы. Следовательно, общее решение исходной системы можно записать и в таком виде: х = (–3, –3, 14, 0, 0) + a(2, 2, –6, 1, 0) + b(2, 2, –7, 0, 1), где a, b – любые.

Нужно обратить внимание и на то, что разность двух частных решений неоднородной системы (–3, –3, 14, 0, 0) – (1, 1, 1, 1, 1) есть решение соответствующей однородной системы уравнений.

§9. «Альтернатива Фредгольма»

Для квадратной системы (j =1, 2, …, п):

а) или система имеет решение, притом единственное при любых b_j, если соответствую­щая однородная система имеет только тривиальное решение (detA ≠0),

б) или соответствующая однородная система имеет ненулевые решения (detA = 0) и, следовательно, есть такие b_j, при которых система не имеет решений.