Критерий Михайлова

Для устойчивости замкнутой системы n-ого порядка необходимо и достаточно чтобы при изменении частоты от 0 до бесконечности вектор Михайлова повернулся на угол nπ/2 нигде не обращаясь в 0.

Вектор Михайлова получается на основании характеристического полинома 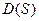, заменим 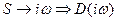или оператора дифференцирования Р на iw получаем:

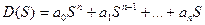
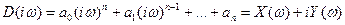–математическая запись вектора Михайлова

С учетом того, что i=Ö-1, i²=Ö-1, (iw)²=-w², (iw)³=-iw³, (iw)⁴=w⁴ и т.д.

четные степени iw вещественны, а нечетные – мнимые.

Тогда вещественная часть

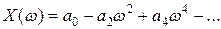
Мнимая часть

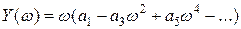
Модуль

Фаза

Замкнутая система устойчива, если при изменении частоты от 0 до ¥ кривая Михайлова будет последовательно проходить через соответствующие четверти комплексной плоскости не проходя через начало координат.

Графически это означает.

Кривая, которая ограничивает вершины вектора Михайлова называется кривой Михайлова.

Замкнутая система устойчива, если при изменении частоты от 0 до бесконечности кривая Михайлова последовательно проходит через соответствующие четверти комплексной плоскости, не проходя при этом через начало координат.

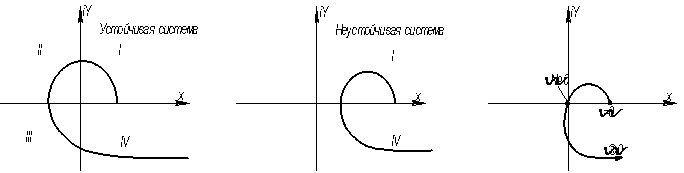
Если годограф проходит меньше чем n квадрантов или при обходе нарушается последовательность перехода из квадранта в квадрант, то система неустойчива. Если годограф проходит через начало координат, то система будет на границе устойчивости.