Устойчивость линейных систем автоматического управления

Под влиянием внешних воздействий в любой системе автоматического управления возникают переходные процессы. Система называется устойчивой, если переходные процессы в ней с течением времени завершаются, и система переходит в новое равновесное состояние или возвращается в прежнее.

Устойчивость – это свойство системы выведенной из состояния равновесия внешними воздействиями и предоставленной самой себе переходить в новое равновесное состояние или возвращаться в прежнее.

Устойчивость – обязательное требование к работоспособной системе.

Уравнение движения САУ имеет вид

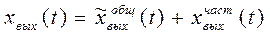
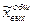- общее решение характеризует свободные колебания (характеризуют переходные процессы)

- частное решение характеризует вынужденный режим (характеризует установившийся режим системы)

Переходный процесс 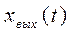зависит как от свойств системы, так и от вида возмущения.

В переходном процессе всегда следует различать две составляющие 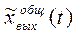- свободные движения системы, определяемые начальными условиями и свойствами самой системы, 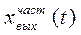- вынужденные движения, определяемые возмущающими воздействиями системы и ее свойствами.

Чтобы САУ могла правильно реагировать на сигнал управления, настройки или изменения нагрузки в переходном процессе, свободная составляющая с течением времени должна стремиться к нулю, т. е.

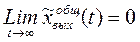- необходимое условие для устойчивости системы.

При аналитическом исследовании динамических свойств САУ необходимо найти ее дифференциальное уравнение и затем его проинтегрировать, т. е. найти закон изменения во времени интересующей величины. Рассмотрим дифференциальное уравнение САУ.

В соответствии с определением устойчивости системы она характеризуется свободными движениями системы. Так как свободное движение системы описывается однородным дифференциальным уравнением, т. е. уравнением без правой части, то следовательно, для определения устойчивости необходимо исследовать это однородное уравнение.

Уравнение свободного движения, разрешенное относительно исследуемой величины, можно записать так:

в операторной форме:

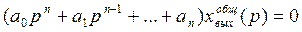
Отсюда характеристическое уравнение имеет вид:

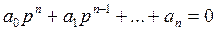
Решение дифференциального уравнения при всех вещественных корнях имеет вид

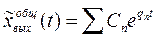(1)

где 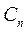- постоянные интегрирования, определяемые параметрами системы и начальными условиями (всегда > 0).

q-корни характеристического уравнения, всегда бывают попарно сопряженными.

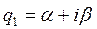
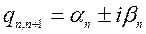
Тогда уравнение (1) в соответствии с формулой Эйлера

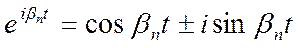
может быть представлено в следующем виде:

где Сn* - начальная амплитуда.

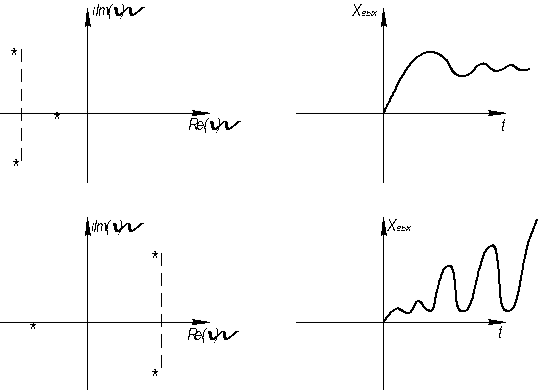
Если α>0, то с течением времени растет амплитуда

α< 0, то с течением времени амплитуда стремится к нулю

α=0 – гармонический процесс

Для определения устойчивости необходимо определить

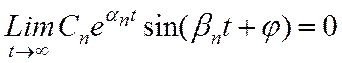
Возможны случаи:

1) α< 0, то предел равен 0 и система устойчива;

2) α< 0, но среди корней имеются нулевые или чисто мнимые корни, то предел стремится к некоторому установившемуся процессу определяемому нулевыми или мнимыми корнями (консервативная система);

3) Если хотя бы одно значение α>0, то предел стремиться к бесконечности, т.е. система неустойчива.

Вывод: Для устойчивости системы необходимо и достаточно, чтобы вещественные части корней характеристического уравнения была отрицательны.