Критерии Найквиста

Замкнутая система устойчива, если АФЧХ соответствующей разомкнутой системы не охватывает точку на комплексной площади с координатами (-1;i) – точка Найквиста.

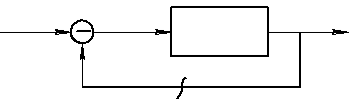
В системе нужно разорвать внешнюю обратную связь.

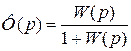
Знаменатель передаточной функции Ф(р) замкнутой автоматической системы представляет собой функцию F(p)=1+W(p) на единицу отличающуюся от передаточной разомкнутой системы W(p)

Замкнутая линейная система устойчива, если приращение фазы функции F(p)=1+W(p) при изменении w от 0 до ¥ равно mπ, где m – число корней характеристического уравнения разомкнутой системы, лежащих на комплексной плоскости справа от мнимой оси.

Так как функция F отличается от КЧХ W на единицу, то для определения приращения фазы нет необходимости строить годограф F, так как эту кривую можно рассматривать как кривую W, если перенести начало координат по вещественной оси влево на единицу.

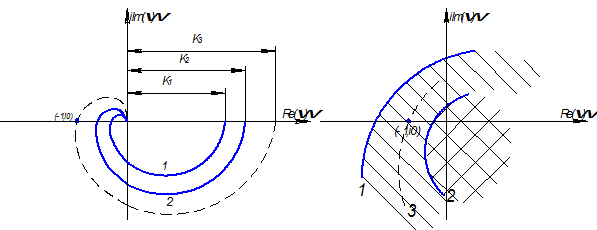
К_1,2 – передаточный коэфф.

1 – система неустойчива

2 – устойчивая система

3 – система, находящаяся на границе устойчивости

Критическим передаточным коэффициентом (К) – называется передаточный коэффициентом системы находящийся на границе устойчивости.

К≥К_КР – неустойчивая система

К≤К_КР – устойчивая система

Для того, что бы обеспечить высокую точность управления передаточный коэффициент статической системы должен быть максимально большим. Однако увеличение передаточного коэффициента приводит к снижению устойчивости системы, это техническое противоречие разрешается при проектировании системы правильным выбором ее конструктивных элементов, через правильный выбор постоянных времени.

Максимально возможный передаточный коэффициентом обеспечивается, если в данной системе обеспечены условия:

1. (Т_МАХ – Т_MIN)→МАХ

2.

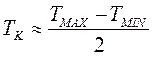
3. Остальные постоянные времени должны быть близки к Т_MIN: Т→Т_MIN