Задание 1. Определение момента инерции маятника Максвелла относительно его оси

1. Надеть на диск кольцо, прижимая его до упора.

2. Нажатием клавиши СЕТЬ включить напряжение питания, при котором высвечиваются лампочки фотоэлектрических датчиков №1 и №2 и циферблат миллисекундомера. Одновременно включается электромагнит.

3. На ось маятника намотать нить подвески, стараясь, чтобы она наматывалась равномерно, виток к витку.

4. Фиксировать маятник при помощи электромагнита, обращая внимание на то, что нить в этом положении не была слишком скручена. Убедиться, что нижняя грань кольца отвечает нулю шкалы на колонке. Чуть повернуть маятник в направлении его движения (на угол около 5^о).

5. Установить нуль миллисекундомера нажатием клавиши СБРОС.

6. Нажать клавишу ПУСК, при этом отключается электромагнит, маятник падает, включается миллисекундомер, идет отсчет времени.

7. Замер времени повторить 5 раз. Все измерения занести в табл. 4.3.

8. Определить значение среднего времени падения.

9. Измерить внешний диаметр оси маятника D.

10. По шкале на вертикальной колонке прибора определить длину маятника h, а по формуле m = m_O + m_D + m_K вычислить массу маятника вместе с кольцом, где m_O – масса оси маятника, m_D – масса диска, m_K – масса кольца. Значения масс отдельных элементов нанесены на них.

11. По формуле (4.27) определить момент инерции маятника J.

12. Все результаты измерений записать в табл. 4.3. Под таблицей выполнить расчеты.

13. При выполнении работы ось маятника должна быть параллельна оси прибора.

14. По формуле 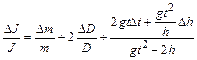оценить погрешность измерения момента инерции.

15. По формуле (4.30) определить расчетное значение момента инерции маятника Максвелла.

16. Сравнить расчетное значение момента инерции с его экспериментальным значением. Сделать выводы.

17. Опыт повторить с другими кольцами.

Таблица 4.3