Теория метода и описание прибора. Метод измерения скорости полета снаряда основан на законе сохранения момента импульса относительно некоторой оси.
Метод измерения скорости полета снаряда основан на законе сохранения момента импульса относительно некоторой оси.
Пусть снаряд массой m, движущийся со скоростью V, попадает в неподвижное уравновешенное твердое тело на расстоянии l от оси вращения и застревает в нем. Применение закона сохранения момента импульса относительно оси вращения дает следующее соотношение
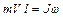 (5.3)
(5.3)
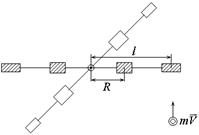 Рис. 5.2
Рис. 5.2
| До столкновения с телом моментом импульса обладал лишь снаряд 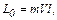 после столкновения после столкновения 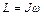 , где , где 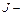 момент инерции тела вместе со снарядом. По закону сохранения момента импульса L0 = L.
Зная m, l, J, w, можно определить скорость снаряда: момент инерции тела вместе со снарядом. По закону сохранения момента импульса L0 = L.
Зная m, l, J, w, можно определить скорость снаряда:
|
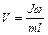 . (5.4)
. (5.4)
Сразу после соударения снаряда крутильный маятник обладает только кинетической энергией
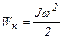 . (5.5)
. (5.5)
По достижении максимального отклонения из положения равновесия маятник останавливается, его кинетическая энергия переходит в потенциальную энергию упругой деформации закрученной проволоки
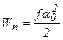 , (5.6)
, (5.6)
где f – модуль кручения проволоки; J – момент инерции маятника вместе со снарядом; 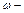 наибольшее значение угловой скорости маятника; a0 – наибольший угол отклонения маятника из положения равновесия.
наибольшее значение угловой скорости маятника; a0 – наибольший угол отклонения маятника из положения равновесия.
Приравнивая выражения (5.5) и (5.6) (по закону сохранения энергии), находим
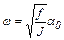 . (5.7)
. (5.7)
Тогда выражение (5.4) для скорости снаряда примет вид
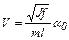 . (5.8)
. (5.8)
С другой стороны, движение маятника после попадания в него снаряда описывается основным законом динамки вращательного движения:
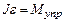 , (5.9)
, (5.9)
где Mупр = – fa – момент сил упругости закрученной проволоки.
Так как угловое ускорение ε – вторая производная от угла поворота a по времени, то мы приходим к дифференциальному уравнению колебательного движения маятника:
 или
или 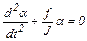 . (5.10)
. (5.10)
Это дифференциальное уравнение свободных незатухающих гармонических колебаний. Решением этого уравнения является функция
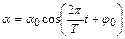 . (5.11)
. (5.11)
Выражение (5.11) будет удовлетворять уравнению (5.10) (в чем можно убедиться непосредственной подстановкой) лишь в том случае, когда
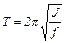 . (5.12)
. (5.12)
Подставляя в (5.8) выражение для момента инерции из (5.12), получим
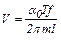 . (5.13)
. (5.13)
Специальная методика измерения скорости V позволяет исключить модуль кручения f из формулы (5.13).
Пусть снаряд был выпущен из стреляющего устройства, когда перемещаемые грузы находились на расстоянии R1 от оси вращения. В этом положении момент инерции маятника
 ,
,
следовательно, период колебаний составит
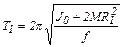 . (5.14)
. (5.14)
После перемещения грузов до расстояния 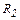 период изменится:
период изменится:
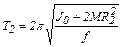 , (5.15)
, (5.15)
где J0 – момент инерции маятника без грузов; M – масса одного груза.
Из соотношений (5.14) и (5.15) можно получить следующее выражение для f:
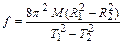 . (5.16)
. (5.16)
Подставляя выражение (5.16) в формулу (5.13) для 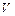 с учетом того, что T = T1, получим
с учетом того, что T = T1, получим
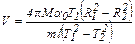 . (5.17)
. (5.17)
В формуле (5.17) величины M, m, l – задаются, а величины T1, T2, R1, R2, a0 измеряются.

|
| Рис. 5.3 |
В настоящей работе для измерения скорости снаряда используется баллистический крутильный маятник ФРМ-09 (рис. 5.3). Он состоит из основания (1), оснащенного регулируемыми ножками (2), которые позволяют устанавливать основание горизонтально. В основании закреплена стойка (3), на которой закреплены верхний (4), нижний (5) и средний (6) кронштейны. К среднему кронштейну прикреплено стреляющее устройство (7), а также прозрачный экран с нанесенной на него угловой шкалой (8) и фотоэлектрический датчик (9). Кронштейны (4) и (5) имеют зажимы, служащие для крепления стальной проволоки (13), на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином (10), двух перемещаемых грузов (11), двух стержней (12) и водилки (14).
Дата добавления: 2015-06-17; просмотров: 794;
