Кинетического момента механической системы
5.3.1. Моменты количества движения
материальной точки относительно центра и оси
Рассмотрим движение материальной точки в горизонтальной плоскости OXY (рис. 5.5).
Момент количества движения m·V точки относительно центра О представляет собой вектор LО, направленный перпендикулярно к плоскости, проходящей через вектор m·V и центр О в ту сторону, откуда видно, что вектор m·V поворачивает горизонтальную плоскость относительно оси, проходящей через центр О, против хода часовой стрелки.

Момент количества движения материальной точки относительно центра – величина, равная векторному произведению радиус-вектора материальной точки, проведенного из этого центра, на количество движения.
Согласно рис. 5.5 момент количества движения LО можно определить векторным произведением радиус-вектора r, проведённого из точки О в точку М, на вектор количества движения m·V:
LО = r×(m·V).
Модуль LО вектора LО равен произведению величины m·V на плечо h вектора m·V относительно центра О:
LО = (m·V)·h.
Плечо h вектора m·V количества движения точки относительно центра – кратчайшее расстояние от точки О до линии действия вектора m·V.
Момент LО количества движения m·V относительно точки О равен нулю в том случае, когда линия действия вектора m·V проходит через точку О, так как тогда плечо h = 0.
Рассмотрим случай движения точки в пространстве (рис. 5.6).

Дадим определение понятия «момент количества движения точки относительно оси».
Момент количества движения точки относительно оси – величина, равная проекции на ось момента количества движения точки относительно любого выбранного на данной оси центра.
Согласно определению имеем:
LОХ = LО·cos(LО, i);
LОY = LО·cos(LО, j);
LОZ = LО·cos(LО, k),
где LОХ, LОY, LОZ – проекция вектора LО на оси ОХ, OY, OZ.
При решении практических задач пользоваться этими формуллами неудобно. Поэтому поступают следующим образом.
Вектор m·V количества движения разлагают на компоненты m·VOX, m·VOY, m·VOZ по соответствующим координатным осям.
Момент количества движения m·V точки относительно оси – величина, равная алгебраической сумме моментов компонентов m·VOX, m·VOY, m·VOZ вектора m·V относительно этой оси.
Если компонента вектора m·V вызывает вращение тела против хода часовой стрелки, то момент количества движения этой компоненты относительно оси положителен, и отрицателен при противоположном условии. При этом на тело необходимо смотреть с положительного направления отсчёта соответствующей координаты.
Аналитические выражения для определения моментов LOX, LOY, LOZ количества движения относительно соответствующих координатных осей OX, OY, OZ имеют вид:
LOX = (m· 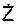 )·Y – (m·
)·Y – (m· 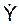 )·Z;
)·Z;
LOY = (m· 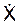 )·Z – (m·
)·Z – (m· 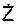 )·X;
)·X;
LOZ = (m· 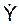 )·X – (m·
)·X – (m· 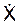 )·Y,
)·Y,
где X, Y, Z – координаты движущейся точки; 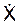 ,
, 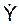 ,
, 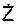 – проекции скорости точки на оси координат.
– проекции скорости точки на оси координат.
5.3.2. Теорема об изменении момента количества
движения материальной точки

Рассмотрим движение материальной точки, входящей в механическую систему, в инерциальной системе отсчёта (рис. 5.7).
Пусть точка движется в горизонтальной плоскости OXY под действием активных сил  , реакций
, реакций  внешних связей и внутренних сил
внешних связей и внутренних сил  .
.
Равнодействующую Р этих сил определяют по формуле
Р = Σ  + Σ
+ Σ  + Σ
+ Σ  .
.
Теорему об изменении момента количества движения материальной точки механической системы выражают векторным равенством:
dLО/dt = ΣMО(  ) + ΣMО(
) + ΣMО(  ) + ΣMО(
) + ΣMО(  ).
).
Производная по времени от момента количества движения материальной точки механической системы относительно некоторого неподвижного центра равна геометрической сумме моментов сил, действующих на точку, относительно того же центра.
Так как проекция векторной производной на любую ось равна производной от её проекции, то, проецируя последнее векторное равенство на координатные оси системы отсчёта OXYZ, получим:
dLOX/dt = ΣMOX( 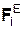 ) + ΣMOX(
) + ΣMOX(  ) + ΣMOX(
) + ΣMOX(  );
);
dLOY/dt = ΣMOY(  ) + ΣMOY(
) + ΣMOY(  ) + ΣMOY(
) + ΣMOY(  );
);
dLOZ/dt = ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  ) + ΣMOZ(
) + ΣMOZ(  ).
).
Производная по времени от момента количества движения материальной точки механической системы относительно некоторой неподвижной оси равна алгебраической сумме моментов сил, действующих на точку, относительно этой же оси.
Дата добавления: 2015-05-30; просмотров: 1816;
