Механической системы. Рассмотрим движение неизменяемой механической системы, находящейся под действием активных сил , реакций внешних связей и внутренних сил в инерциальной

Рассмотрим движение неизменяемой механической системы, находящейся под действием активных сил , реакций внешних связей и внутренних сил в инерциальной системе отсчёта ОXYZ (рис. 5.1).

Поскольку главный вектор внутренних сил 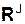= Σ = 0, то теорема о движении центра масснеизменяемоймеханической системы выражается векторным равенством:

m·a_c = Σ + Σ = F^E + R^E,

где F^E = Σ – главный вектор активных сил; R^E = Σ – главный вектор реакций внешних связей.

Произведение массы механической системы на ускорение её центра масс равно геометрической сумме приложенных к ней активных сил и реакций внешних связей.

Таким образом, центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены внешние силы (активные силы и реакции внешних связей).

Проецированием последнего векторного равенства на координатные оси системы отсчёта OXYZ получим дифференциальные уравнения движения центра масс механической системы:

m· 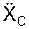= Σ + Σ ;

m· = Σ + Σ ;

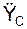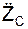m· = Σ + Σ ,

где Σ , Σ , Σ , Σ , Σ , Σ – суммы проекций соответственно активных сил и реакций внешних связей на координатные оси инерциальной системы отсчёта.

Из последних уравнений следует, что внутренние силы не влияют на движение центра масс неизменяемой механической системы.