Центр масс механической системы
Напомним некоторые понятия, которые широко применяются в этом учебно-методическом пособии.
Механической системой называют такую совокупность материальных точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.
Механическую систему, движение которой не ограничено связями, а определяется только действующими на неё силами, называют свободной механической системой.
Механическая система, движение которой ограничивается наложенными на её точки внешними связями, называется несвободной механической системой.
Все силы, действующие на точки механической системы, делят на внешние и внутренние силы.
Внешними называют силы, действующие на точки данной механической системы со стороны материальных тел, не входящих в данную механическую систему.
К внешним силам относятся активные (задаваемые) силы и реакции внешних связей. Активные силы условимся обозначать  , реакции внешних связей –
, реакции внешних связей –  .
.
Внутренними силами называют силы взаимодействия между точками данной механической системы. Внутренние силы условимся обозначать  .
.
Неизменяемая механическая система – механическая система, в которой материальные точки имеют постоянные массы, а связи между точками не деформируются.
Следует отметить, что в данном учебно-методическом пособии рассматриваются только неизменяемые механические системы.
Движение точек механической системы зависит от активных сил  , реакций внешних связей
, реакций внешних связей  и внутренних сил
и внутренних сил  .
.
Рассмотрим движение несвободной механической системы в инерциальной системе отсчёта OXYZ (рис. 4.1).
На рис. 4.1 использованы следующие обозначения: VCi, aCi – скорость и ускорение центра Ci тяжести i-й точки механической системы;  ,
,  ,
,  – соответственно активная сила, реакция внешней связи, внутренняя сила, приложенные к i-й точке механической системы; XCi, YCi, ZCi – координаты конца радиус-вектора rCi центра тяжести i-й точки механической системы; VC, aC – скорость, ускорение центра масс механической системы;
– соответственно активная сила, реакция внешней связи, внутренняя сила, приложенные к i-й точке механической системы; XCi, YCi, ZCi – координаты конца радиус-вектора rCi центра тяжести i-й точки механической системы; VC, aC – скорость, ускорение центра масс механической системы; 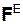 = Σ
= Σ  ,
, 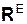 = Σ
= Σ  ,
, 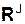 = Σ
= Σ  – соответственно главные векторы активных сил, реакций внешних связей, внутренних сил; XC, YC, ZC – координаты конца радиус-вектора rC центра масс механической системы.
– соответственно главные векторы активных сил, реакций внешних связей, внутренних сил; XC, YC, ZC – координаты конца радиус-вектора rC центра масс механической системы.

Необходимо отметить, что для неизменяемых механических систем главный вектор внутренних сил 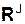 = Σ
= Σ  всегда равен нулю (
всегда равен нулю ( 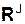 = 0).
= 0).
Каждая i-я точка механической системы имеет определённую массу mCi , а её положение в системе отсчёта OXYZ в любой момент времени определяется радиус-вектором rCi или тремя координатами: XCi, YCi, ZCi.
За центр масс механической системы принимают геометрическую точку С, радиус-вектор которой равен
rC = ΣmCi·rCi/m,
где m – масса механической системы.
Массу m механической системы определяют по формуле
m = ΣmCi.
Центр масс механической системы – геометрическая точка, для которой сумма произведений масс всех материальных точек, образующих механическую систему, на их радиус-векторы, проведенные из этой точки, равна нулю.
Проецируя векторное равенство rC = ΣmCi·rCi/m на координатные оси системы отсчёта OXYZ, получим формулы, определяющие координаты центра масс механической системы:
XC = ΣmCi·XCi/m;
YC = ΣmCi·YCi/m;
ZC = ΣmCi·ZCi/m.
Эти формулы называют уравнениями движения центра масс механической системы.
Как видно из последних формул, положение центра масс механической системы в любой момент времени зависит только от положения и массы каждой точки этой системы.
Центр тяжести системы тел совпадает с их центром масс. Понятие «центр масс механической системы» более широкое по сравнению с понятием «центр тяжести», так как последнее понятие применяется только для твёрдого тела или системы твёрдых тел, находящихся в однородном поле сил тяжести.
Дифференцируя по времени векторное равенство rC = ΣmCi·rCi/m, несложно определить векторы скорости VС и ускорения aС центра масс механической системы, их проекции на координатные оси, модули и направляющие косинусы:
VC = drC/dt = ΣmCi·VСi/m;
aC = d2rC/dt2 = ΣmCi ·aCi/m;
XC = ΣmCi·XCi/m;
YC = ΣmCi·YCi/m;
ZC = ΣmCi·ZCi/m;
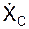 = ΣmCi·
= ΣmCi· 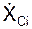 /m;
/m;
 = ΣmCi·
= ΣmCi· 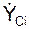 /m;
/m;
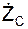 = ΣmCi·
= ΣmCi· 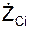 /m;
/m;
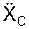 = ΣmCi·
= ΣmCi· 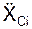 /m;
/m;
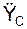 = ΣmCi·
= ΣmCi· 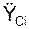 /m;
/m;
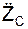 = ΣmCi·
= ΣmCi· 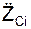 /m;
/m;
VC = 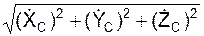 ;
;
aC = 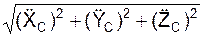 ;
;
cos(VC, i) = 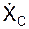 / VC;
/ VC;
cos(VC, j) =  / VC;
/ VC;
cos(VC, k) = 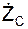 / VC;
/ VC;
cos(aC, i)= 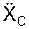 /aC;
/aC;
cos(aC, j)= 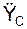 /aC;
/aC;
cos(aC, k)= 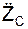 /aC.
/aC.
Дата добавления: 2015-05-30; просмотров: 7685;
