Амплитудно-модулированные сигналы и их спектры

При амплитудной модуляции (АМ) амплитуда несущего сигнала подвергается воздействию сигнала сообщения. Мгновенное значение АМ колебания с гармонической несущей может быть записано в виде

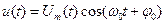, (2.16)

где U_m(t) – «переменная амплитуда» или огибающая амплитуд;

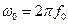– круговая частота несущего сигнала;

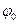– начальная фаза несущего сигнала.

«Переменная амплитуда» U_m(t) пропорциональна управляющему сигналу (сигналу сообщения) U_с(t):

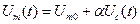, (2.17)

где U_m0 – амплитуда несущего сигнала до амплитудной модуляции, то есть поступающего на модулятор;

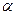– коэффициент пропорциональности.

При модуляции несущего сигнала сигналом сообщения необходимо обеспечить, чтобы U_m(t) была величиной положительной. Это требование выполняется выбором коэффициента .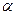

Для исключения влияния переходных процессов в радиоэлектронной цепи модулятора и других цепях преобразования модулированного сигнала на спектр сигнала сообщения необходимо выполнение следующего условия: наивысшая по частоте спектральная составляющая в ограниченном спектре сигнала сообщения должна иметь частоту 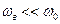, – что обеспечивается выбором частоты несущего сигнала.

a)		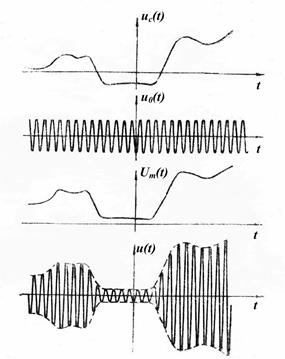a)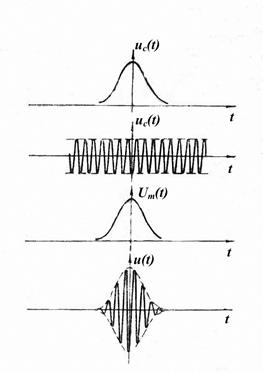
б)	б)
в)	в)
г)	г)
Рис. 2.10. Амплитудная модуляция непрерывным сигналом сообщения	Рис. 2.11. Амплитудная модуляция видеоимпульсом

На рис. 2.10 и 2.11 показаны два примера построения графиков АМ колебаний. На рисунках изображены следующие графики:

а – сигнал сообщения u_c(t);

б – несущий сигнал u₀(t);

в – огибающая амплитуд U_m(t);

г – АМ сигнал u(t).

Для понимания образования спектра АМ сигнала рассмотрим простой случай: однотональное амплитудно-модулированное колебание. В этом случае модулирующий сигнал является гармоническим (однотональным):

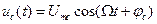
с амплитудой U_mc, частотой 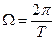и начальной фазой .

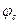Огибающая амплитуд однотонального АМ колебания имеет вид:

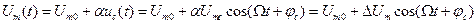, (2.18)

где 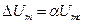– максимальное приращение амплитуды. Мгновенное значение однотонального АМ колебания

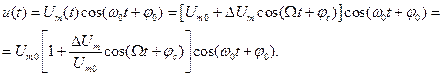
Отношение 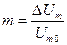называется коэффициентом глубины модуляции или просто коэффициентом модуляции. Так как U_m(t)>0, то 0<m<1. Часто m измеряют в процентах, тогда 0<m<100%. С учетом введения коэффициента модуляции однотональное модулированное колебание запишем в виде:

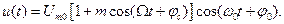(2.19)

Графики, поясняющие процесс однотональной амплитудной модуляции, приведены на рис. 2.12.

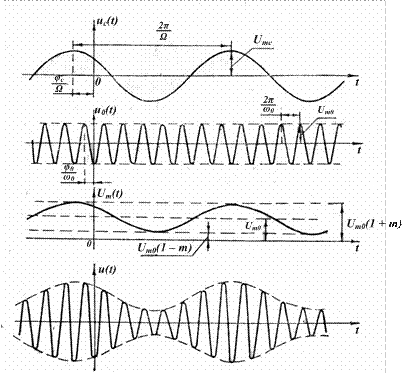
Рис. 2.12. Однотональная амплитудная модуляция

Для нахождения спектра однотонального амплитудно-модулированного сигнала необходимо сделать следующие преобразования:

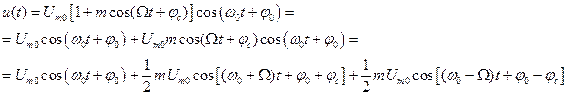(2.20)

При выводе выражения (2.20) использована тригонометрическая формула

.

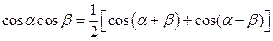Таким образом, при однотональной амплитудной модуляции несущего сигнала спектр содержит три составляющие: одна на несущей частоте 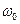имеет амплитуду U_m0 и две на боковых частотах 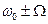с амплитудами mU_m0/2, зависящими от коэффициента модуляции; при m<1 их амплитуды составляют не более половины амплитуды несущей гармоники. Начальные фазы колебаний боковых спектральных составляющих отличаются от начальной фазы на величину . На рис. 2.13 показаны графики АЧС и ФЧС однотонального амплитудно-модулированного колебания.

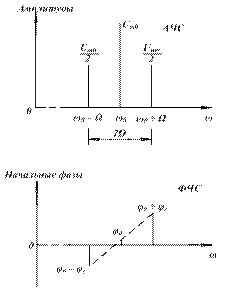
Рис. 2.13. Спектр однотонального амплитудно-модулированного колебания

Из анализа спектра следует, что АЧС является четным относительно частоты 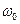, а ФЧС нечетным относительно точки с координатами ( , ).

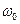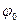При условии 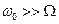все составляющие спектра являются высокочастотными, следовательно, такой сигнал может эффективно передаваться с помощью ЭМВ.

Рассмотрим энергетические параметры однотонального АМ сигнала. Средняя за период несущего сигнала мощность, выделяемая на единичном сопротивлении,

.

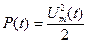В отсутствии модуляции эта мощность равна

,

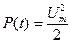а при модуляции изменяется в пределах от

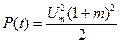
до

.

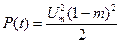Если m=100%, то 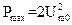, а P_min = 0. Средняя мощность сигнала за период модуляции будет складываться из мощностей спектральных составляющих

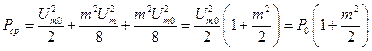. (2.21)

В случае m=100% Р_ср = 1,5Р₀.

Перейдем к рассмотрению общего случая к так называемому многотональному АМ сигналу. Модулирующий сигнал, то есть сигнал сообщения, имеет спектр вида (1.22)

.

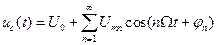Огибающая амплитуд имеет вид:

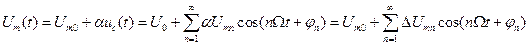, (2.22)

где 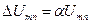– максимальное приращение амплитуды n-ой гармоники модулирующего сигнала.

Выражение для многотонального АМ сигнала примет следующий вид:

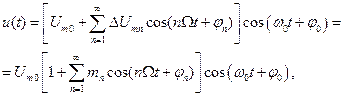(2.23)

где 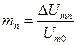– коэффициент модуляции n-ой гармоники модулирующего сигнала. Применяя аналогичные, как это было сделано для однотональной амплитудной модуляции, тригонометрические преобразования, получим

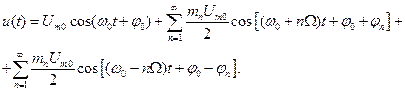(2.24)

Выражение (2.24) представляет спектр амплитудно-модулированного сигнала. Относительно колебания с частотой 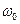имеют место два ряда составляющих с верхними 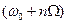и нижними 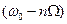боковыми частотами. Эти составляющие образуют так называемые верхнюю и нижнюю боковые полосы спектра.

Передать весь спектр АМ сигнала по каналу информации невозможно по следующим причинам. Во-первых, нельзя создать идеальную линейную цепь в области частот 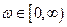, см. п.1.4. Во-вторых, при увеличении полосы пропускания линейной цепи может уменьшиться отношение мощности сигнала к мощности шумов (см. п.1.5). В-третьих, полоса пропускания, по возможности, должна быть минимальной, чтобы в заданном частотном диапазоне работало как можно больше радиолиний (радиоканалов), не влияющих друг на друга, то есть не создающих друг другу помех. Следовательно, спектр сигнал ограничивается частотой 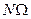, наиболее удаленной от частоты 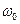несущего сигнала. На рис. 2.14 приведенный амплитудный спектр АМ сигнала. Ширина спектра определяется максимальной частотой в спектре модулирующего сигнала 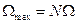и составляет 2 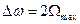. Примерные значения ширины спектра для некоторых АМ сигналов представлены в табл. 1.1.

Таблица 1.1

Примерные значения ширины спектра

Рис. 2.14. Амплитудный спектр многотонального АМ сигнала

Очевидно, что в выражении (2.24) можно одну из сумм убрать, при этом оставшаяся часть полностью описывает сигнал сообщения. Такой спектр называется однополосным, а каналы, реализующие передачу АМ сигнала, – однополюсными радиоканалами. Для того, чтобы радиоканал меньше влиял на спектр сигнала сообщения, передают верхнюю боковую полосу вместе с гармоникой на несущей частоте:

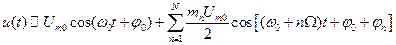. (2.25)

Исходя из выражения (2.21), по аналогии заключаем, что при однополюсной передаче АМ-сигнала средняя мощность сигнала за период модуляции будет примерно в два раза меньше, чем при передаче обеих полос, то есть всего спектра сигнала (2.24). Однако, этот недостаток легко устраним усилением по мощности модулированного сигнала.

Таким образом, полоса пропускания радиоканала

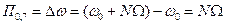. (2.26)

В этой полосе частот амплитудно-частотная и фазо-частотная характеристики радиоканала должны удовлетворять требованиям линейной цепи (п.1.4).