Сигналы при фазовой и частотной модуляциях

При фазовой модуляции (ФМ) имеет место воздействие сигнала сообщения на начальную фазу несущего сигнала, а при частотной модуляции (ЧМ) это воздействие осуществляется на частоту несущего сигнала.

У ФМ сигнала с гармонической функцией начальная фаза становится функцией времени:

,

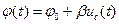где 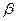– коэффициент пропорциональности. Мгновенное значение ФМ сигнала имеет вид

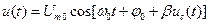. (2.28)

Полная фаза такого колебания

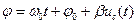(2.29)

изменяется в общем случае нелинейно. Мгновенное значение частоты колебаний находится как производная по времени полной фазы:

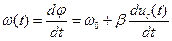, (2.30)

при этом значение 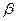должно быть таким, чтобы было обеспечено неравенство 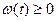для любого момента времени.

При частотной модуляции частота несущего сигнала

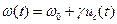, (2.31)

где 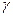– коэффициент пропорциональности, обеспечивающий 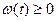для любого t. Полная фаза находится путем интегрирования (2.31)

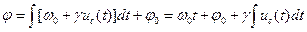. (2.32)

Следовательно, аналитическая форма записи ЧМ сигнала имеет вид

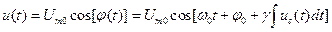. (2.33)

Вначале рассмотрим однотональную частотную модуляцию несущего сигнала. В этом случае сигнал сообщения

.

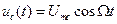Тогда

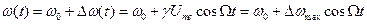, (2.34)

где 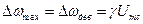– максимальное изменение (или девиация – от лат. deviatio – уклонение) частоты.

С учетом (2.34) выражение (2.32) запишем в виде

,

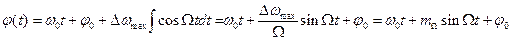где 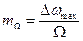– индекс частотной модуляции. Выбирая отсчет времени так, чтобы при t=0 значение 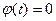, получим 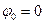. Тогда

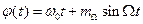, (2.35)

а частотно-модулированный сигнал примет следующий аналитический вид

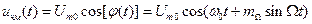. (2.36)

Применяя тригонометрическое преобразование

,

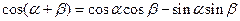выражение (2.36) примет вид

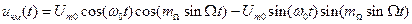. (2.37)

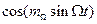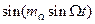Для нахождения спектра ЧМ сигнала необходимо множители и в выражении (2.37) разложить в ряд Фурье. При этом коэффициенты ряда будут функции Бесселя 1-го рода n-го порядка 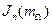, аргументом которых является индекс частотной модуляции:

;

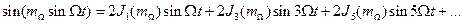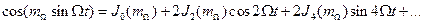. (2.38)

Функции Бесселя табуированы [7]. Графики функций Бесселя первого рода n-го порядка 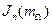изображены на рис. 2.16.

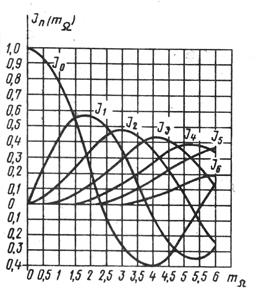
Рис .2.16. График функции Бесселя 1-го рода n-го порядка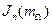

Подставляя (2.38) в (2.37) и преобразовав члены с произведениями тригонометрических функций по формулам

,

,

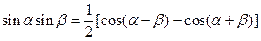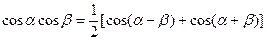получим спектр ЧМ сигнала:

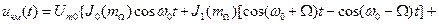
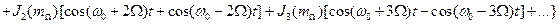. (2.39)

Из выражения (2.39) следует, что спектр ЧМ сигнала при однотональной модуляции содержит бесконечное число составляющих с частотами 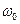, , 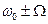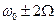и т.д. Амплитуды гармонических составляющих спектра определяются функциями Бесселя 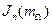. При больших значениях 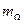амплитуды боковых составляющих превосходят амплитуду на частоте 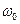. Эта амплитуда определяется функцие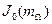й и при 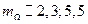близка к нулю. Следовательно, частотная модуляция позволяет сосредоточить большую долю энергии сигнала в боковых составляющих. Это свойство является преимуществом ЧМ сигнала перед АМ сигналом.

При малых значениях индекса частотной модуляции 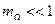в выражении (2.37) 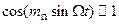, 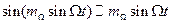. Тогда

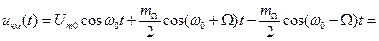
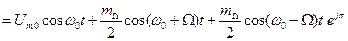. (2.40)

Таким образом, при 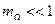амплитудно-частотный спектр ЧМ сигнала такой же, как и спектр АМ сигнала. Фазо-частотный спектр будет иметь отличие: левые боковые составляющие относительно несущей спектральной составляющей будут иметь фазовые сдвиги, равные .

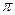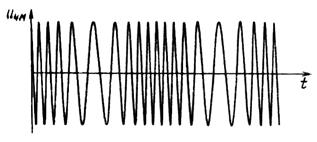
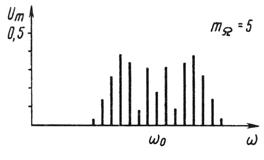
На рис. 2.17 показаны частотно-модулированный сигнал и его спектр при 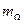= 5. Спектр содержит несущую спектральную составляющую на частоте 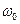и боковые спектральные составляющие на частотах 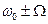, , 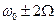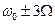и т.д.

а)	б)

Рис. 2.17: а – частотно-модулированный сигнал; б – амплитудно-частотный спектр ЧМ сигнала при 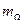= 5

В радиоэлектронных устройствах частотная модуляция несущего сигнала реализуется при 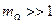. С увеличением 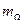спектр ЧМ сигнала расширяется. Однако, при каждом значении 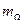участок спектра, занятый относительно спектральной составляющей с максимальной амплитудой, практически ограничен. Принято считать, что ЧМ сигнал достаточно точно воспроизводится спектральными составляющими боковых полос, число которых равно 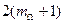. В это число входит несущая спектральная составляющая. Эти составляющие занимают частотную полосу

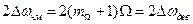, (2.41)

где 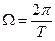– частота повторения.

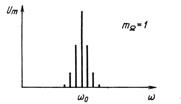
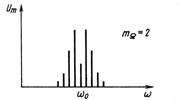
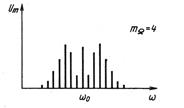
На рис. 2.18 показаны амплитудно-частотные спектры ЧМ сигнала при увеличении индекса частотной модуляции.

Рис. 2.18. Амплитудно-частотные спектры ЧМ сигнала при увеличении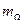

В случае реального сигнала сообщения спектр ЧМ сигнала является более сложным, так как каждой гармонической составляющей сигнала сообщения соответствует своя серия боковых спектральных составляющих ЧМ сигнала. Из (2.41) следует, что при 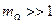для передачи сообщения с помощью ЧМ сигнала с наибольшей частотой 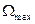(в спектре сигнала сообщения) требуется полоса частот

,

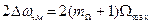существенно большая, чем при АМ сигнале, где эта полоса равна 2 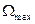. В силу этого частотная модуляция применяется в области высоких частот, так как отношение 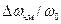с увеличением частоты несущего сигнала 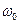уменьшается, и обеспечить заданную полосу частот представляется возможным.

Основным преимуществом ЧМ перед АМ является лучшая помехозащищенность канала радиосвязи, так как помехи в основном воздействуют на амплитуду колебаний, в то время как сообщение об информации содержится в изменении частоты ЧМ сигнала.

Фазовая модуляция во многом похожа на частотную. Как при ФМ, так и при ЧМ меняется полная фаза выражения (2.29) и (2.32), поэтому ту и другую модуляцию называют угловой модуляцией.