Преобразование спектра нелинейным элементом

Пусть имеет место некоторый нелинейный элемент, вольт амперная характеристика которого I=F(U) показана на рис. 2.28. Если функция F(U) дифференцируется, то она может быть представлена следующим степенным полиномом в окрестности точки U₀:

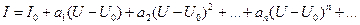. (2.54)

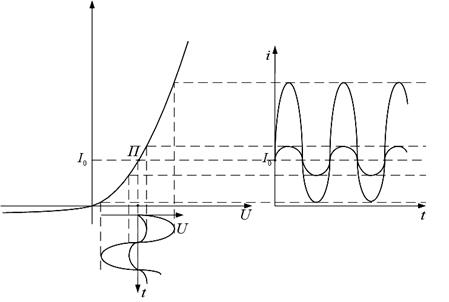
Рис. 2.28. Вольт-амперная характеристика нелинейного элемента (например, полупроводникового диода)

Выберем на этой характеристике некоторую точку покоя П, с координатами (U₀I₀). Относительно напряжения U₀ подадим гармоническое напряжение U(t)=U_m 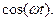Переменное напряжение вызовет изменение во времени тока через нелинейный элемент. Если амплитуда U_m настолькомала, что нелинейностью ВАХ можно пренебречь, то ток во времени будет также изменяться по гармоническому закону.

Если амплитуда U_m такова, что проявляется квадратичный характер ВАХ

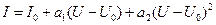, (2.55)

то ток во времени будет иметь более сложный характер изменения:

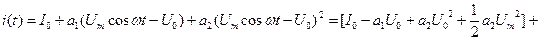
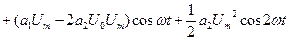. (2.56)

Под действием гармонического напряжения появилась гармоника удвоенной частоты 2ω.

Таким же способом можно убедиться в том, что если вольт-амперная характеристика аппроксимируется полиномом n-ой степени, то гармоническое напряжение вызовет негармонический ток, в спектре которого будут гармоники кратные частоте ω. Эта кратность следует из ранее рассмотренных спектров периодических сигналов. Действительно, функция i(t) является периодической. 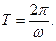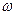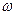Период Следовательно, спектральные составляющие имеют частоты , 2 , 3 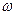, … , n 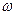, … . Важность записи ВАХ в виде степенного полинома (2.54) в том, что представляется возможность вычисления амплитуд спектральных составляющих. При этом коэффициенты a₁, a₂, a₃, … , a_n, входящие в выражение (2.54), определяются дифференцированием функции I=F(U):

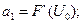
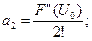
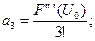… . (2.57)

Пример: на рис. 2.28 представлена ВАХ полупроводникового диода, аналитический вид которой описывается выражением

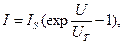
где 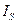- тепловой (или обратный) ток; 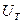- тепловой потенциал.

Вычисляем коэффициенты:

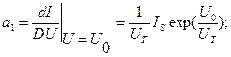
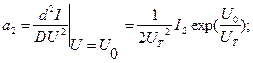
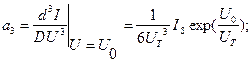
и т.д.

Выражение (2.56) запишем в виде:

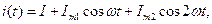(2.58)

где ;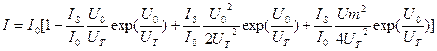

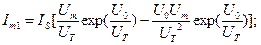
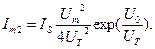
При температуре T=300K тепловой потенциал 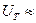0,0256В. Для определения других параметров, входящих в выражения для постоянной составляющей и амплитуд гармоник тока, необходимо выбрать конкретный диод. Если смещение 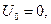то величины, входящие в (2.58) вычисляются по следующим выражениям:

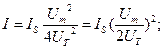
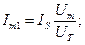
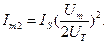
В этом случае значения постоянной (нулевой) составляющей и второй гармоники будут одинаковыми, а амплитуда 1-й гармоники будет или больше амплитуды 2-й гармоники (при 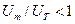), или меньше амплитуды 2-й гармоники ( 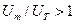). Если 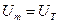, то

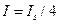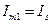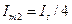, , , (2.59)

Выражения для токов (2.59) можно применить для нахождения значения теплового тока 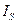экспериментальным путем.

Рассмотрим случай, когда на нелинейный элемент (нелинейное сопротивление) действуют два напряжения с разными частотами:

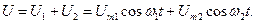
Будем полагать амплитуды этих напряжений такими, что полином (2.54) может быть ограничен первыми тремя членами (2.55). Кроме того примем смещение U₀ = 0. Тогда имеем

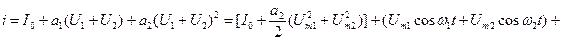
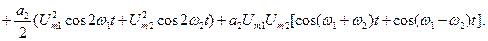(2.60)

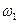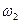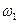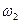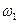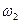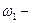
В этом случае в спектре тока появились гармоники с частотами , , 2 , 2 , ( + ), ( )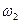. Такие частоты называются комбинационными.

При более сложном виде нелинейности ВАХ, когда приходится использовать полином (2.54) более высокой степени, или при более сложном сигнале, спектр значительно усложняется. При воздействии двух гармонических напряжений на нелинейное сопротивление, ВАХ которого аппроксимируется полиномом k-ой степени, в составе тока образуются частоты, выражаемые соотношением

,

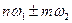где n и m любые целые числа, не исключая нуля.

Из приведённого рассмотрения преобразований спектра сигнала нелинейным элементом можно сделать следующие выводы:

1. В нелинейных системах спектр тока по сравнению со спектром приложенного напряжения существенно обогащён из-за нарушения принципа суперпозиции. Это даёт возможность в генераторах электромагнитных колебаний увеличивать кратно частоту (см. генераторы с внешним возбуждением в режиме умножения частоты входного сигнала); в радиоприёмных устройствах осуществлять перенос спектра сигнала из области высоких частот в область промежуточных частот для улучшения радиотехнических характеристик приёмных устройств и радиолинии в целом;

2. Строгий анализ процессов в нелинейных системах крайне сложен. С помощью аппроксимации ВАХ анализ существенно упрощается, при этом основные моменты изучаемых процессов сохраняются. Такой способ изучения свойств нелинейных систем называется графо-аналитический;

3. Нелинейное сопротивление (элемент) может быть использован не только в существенно нелинейном режиме, когда спектр сигнала с его помощью меняется с целью решения конкретных задач, но и как линейный элемент, например, в усилителях для увеличения энергии сигнала при неизменном составе его спектра.