Принцип Франка-Кондона.

Чтобы оценить вероятность переходов между вибронными уровнями в молекуле, применяется эмпирический принцип, известный под названием Франка-Кондона. Основное положение этого принципа таково: из-за малой массы электронов электронный переход происходит гораздо быстрее колебательного, так что за время электронного перехода относительное положение ядер и скорости ядер не изменяются.

Принцип Франка-Кондона можно обосновать, исходя из вероятностей переходов в 1 сек для переходов между различными уровнями молекул. В литературе обычно приводится расчет вероятности (в сек) спонтанного перехода между электронными уровнями. Эта вероятность определяется коэффициентом Эйнштейна и равна примерно 10-8 сек. В книгах по люминесценции (см. С.Паркер “Фотолюминесценция растворов”) для времени перехода, отвечающего поглощению кванта света, приводится величина 10-15 сек, соответствующая периоду падающего света. Однако известно, что вероятность в 1 сек вынужденного перехода, происходящего при поглощении света, зависит от интенсивности поглощенного света. Эта вероятность может быть рассчитана с помощью коэффициента Эйнштейна В (для вынужденного перехода) для конкретной интенсивности поглощенного света. Из коэффициентов Эйнштейна можно также получить оценку времени перехода между колебательными уровнями, т.е. время колебательной релаксации (10-12 сек).

При этом необходимо отметить, что правильная оценка длительности электронного перехода снизу вверх при поглощении света получится, если на одну молекулу будет падать не меньше одного кванта в 1 сек, т.е. скорость перехода не будет ограничена числом квантов, поглощенных в единицу времени.

Кроме того, надо иметь в виду, что при такой оценке получается максимальное значение длительности процесса перехода, поскольку вероятность перехода в 1 сек описывает изменение состояния системы из начального состояния в конечное и не может указать начало процесса перехода и его длительность.

Рассмотрим следствия принципа Франка-Кондона. Наиболее вероятными являются такие переходы, при которых конфигурация ядер не изменяется, поэтому симметрия колебаний нижнего и верхнего (мгновенного) вибронных уровней должны совпадать. Поскольку симметрия мгновенного верхнего уровня, на который произошел переход, может отличаться от симметрии равновесного уровня, то после электронного перехода возникает перестройка ядерной конфигурации. В соответствии с вышесказанным переход между вибронными уровнями обозначается вертикальной стрелкой (R=const), что и показано на рис. 8.

Принцип Франка-Кондона можно пояснить, используя адиабатическое приближение и следующие предположения: 1) независимость электронных и ядерных движений, 2) дипольный момент чисто электронного перехода не зависит от колебательных координат, 3) разные нормальные колебания не взаимодействуют между собой.

Следовательно, можно написать следующие соотношения:

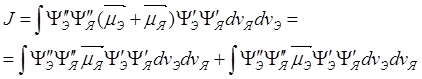(3.1)

Первое слагаемое в (3.1) обращается в нуль из-за ортогональности электронных функций, а второе – можно представить в виде:

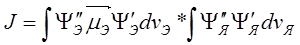(3.2)

Первое слагаемое в (3.2) — электронный дипольный момент перехода, а второе — интеграл перекрывания колебательных функций в нижнем и верхнем электронных состояниях.

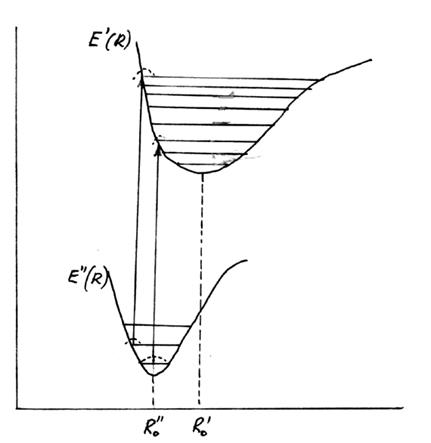
Интеграл перекрывания колебательных функций имеет максимальное значение при равенстве функций Ψ»я и Ψ'я . Максимальные значения колебательных волновых функций в разных колебательных состояниях показаны пунктиром (рис. 8). Используя принцип Франка-Кондона, можно качественно определить наиболее вероятные вибронные переходы.