Свойства электромагнитных волн

В предыдущем параграфе мы видели, что в электромагнитной волне векторы Е и Н перпендикулярны друг другу. Но кроме того они еще и перпендикулярны направлению распространения волны (которое тоже есть вектор). Взаимные расположения этих трех векторов в любой точке бегущей электромагнитной волны связаны правилом правого винта: если головку винта расположить в плоскости векторов Е и Н и поворачивать ее в направлении от Е к Н (по кратчайшему пути), то поступательное движение винта укажет направление распространения волны. Итак, векторы Е и Н колеблются в плоскости, перпендикулярной к направлению распространения. Это означает, что электромагнитные волны являются поперечными волнами. Расположение векторов Е и Н в различных точках волны для одного и того же момента времени показано на рис 2.1.

Как уже упоминалось, электрическое и магнитное поля в электромагнитной волне взаимно связаны друг с другом. Поэтому между мгновенными значениями Е и Н в любой точке существует определенное соотношение, которое также можно найти из уравнений Максвелла.

Для этого заметим, что любая функция вида

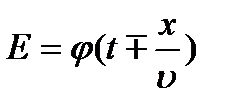(2.1)

удовлетворяет волновому уравнению (1.6). Знак минус при этом относится к волне, распространяющейся в положительном направлении оси ОХ, а знак плюс – в отрицательном. Аналогично и для Н:

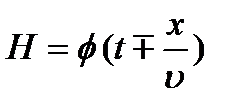(2.2)

Понятно, что вид функции здесь другой. Важно подчеркнуть, что характер зависимости, как Е, так и Н от времени t и координаты х в бегущей волне не какой попало. Время и координата входят только в комбинации

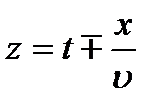(2.3)

Если посмотреть с такой точки зрения, то это означает, что Е и Н зависят только от одной переменной z, которая конечно связана с t и х соотношением (2.3).Если для определенности в (2.3) выбрать, например знак минус (что, как мы уже знаем, соответствует волне идущей вправо), то легко видеть:

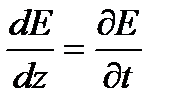и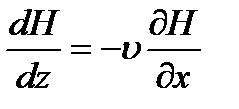

Вспоминая (1.5) получаем:

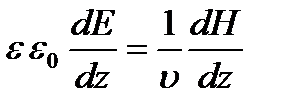или ,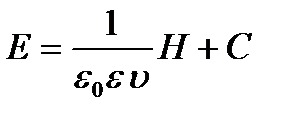

где С обозначает постоянную интегрирования. Так как нас интересуют электромагнитные волны, т. е. только переменные поля, то С, которое выражает произвольное постоянное поле, можно не учитывать. Заменяя еще υ его выражением (1.7), находим окончательно

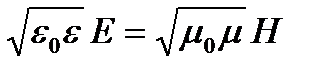(2.4)

Эта формула показывает, что в распространяющейся электромагнитной волне Е и Н пропорциональны друг другу.

Из (2.4) следует, что Е и Н одновременно достигают максимума и одновременно обращаются в нуль, т. е. находятся в фазе.