Линию, вдоль которой происходит распространение фронта волны, называют лучом.

Нетрудно сообразить, что в изотропной среде луч всегда нормален (перпендикулярен) к волновой поверхности. В изотропной среде все лучи представляют собой прямые линии. Каждая прямая, соединяющая точку, в которой находится источник волны, с любой точкой фронта волны, в этом случае является лучом.

Перемещение фронта волны в такой среде происходит с постоянной скоростью, поэтому за один период колебаний источника, создающего волны, фронт волны перемещается на строго определенное расстояние λ. Поскольку каждая точка в волне совершает вынужденные колебания, частота этих колебаний равна частоте колебаний источника волны.

Величину λ, характеризующую перемещение волновой поверхности за один период в зависимости от рода среды и частоты колебаний, называют длиной волны. Длину волны измеряют расстоянием, на которое перемещается, волновая поверхность за один период колебаний источника волн.

Другими словами, учитывая изложенное в § 1, можно сказать (см. рис. 1.2), что длиной волны является расстояние между двумя ближайшими точками бегущей волны на одном луче, которые колеблются в одинаковой фазе. (Докажите, что в расстоянии между двумя любыми точками бегущей волны, которые находятся на одном луче и колеблются в одинаковой фазе, всегда содержится целое число длин волн или четное число полуволн. Если же на луче взять две точки, колеблющиеся в противоположных фазах, то в расстоянии между ними всегда будет содержаться нечетное число полуволн.)

Для поперечных волн (см. рис. 1.3б) длиной волны является кратчайшее расстояние между двумя ближайшими выпуклостями или впадинами. Для продольных волн (см. рис. 1.3а) длиной волны служит кратчайшее расстояние между центрами двух соседних сгущений или разрежений.

Вспомним, что при распространении колебаний в среде происходит перемещение фазы (см. § 1). Скорость распространения колебаний в упругой среде называют фазовой скоростью волны. Так как фазовая скорость c в изотропной среде постоянна, то ее можно найти, разделив перемещение фазы волны на время, за которое оно произошло. Поскольку за время Т фаза волны перемещается на расстояние λ, то

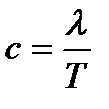
Так как Т=1/ν, где ν – частота колебаний частиц в волне, имеем

(2.1)

Установлено, что в большинстве реально существующих сред фазовая скорость определяется только физическими свойствами среды и ее состоянием. Поэтому механические волны с разной частотой колебаний в заданном веществе распространяются с одинаковой скоростью (заметим, что это верно только при не очень большом различии в частоте колебаний).

Таким образом, определенной частоте колебаний ν в заданной среде соответствует единственное значение длины волны λ. При этом, как видно из формулы (2.1), большей частоте соответствуют более короткие волны в среде. Это дает возможность характеризовать волны в среде не частотой (периодом) колебаний частиц в них, а длиной волны λ. Здесь нужно помнить, что при переходе волны из одной среды в другую частота ν и период колебаний Т частиц в ней остаются постоянными, а длина волны λ изменяется в соответствии с изменением скорости V.

Заметим, что при уменьшении фазовой скорости пропорционально ей уменьшается и длина волны. Итак, характеризовать волны их длиной можно только тогда, когда все сравниваемые волны распространяются в одной и той же среде.

В предыдущем параграфе мы выяснили, что существуют два различных волновых движения: продольное и поперечное. В продольной волне, подобной звуковой волне, частицы среды, сквозь которую распространяются волны, колеблются вперед и назад параллельно направлению распространения волны. В поперечной волне, подобной волнам на веревке, показанным на рис. 2.1, частицы колеблются перпендикулярно к направлению распространения волн.

Зная отличительные черты каждого типа воли, мы можем определить природу волны в каждом случае. Мы знаем, что продольная волна, подобно звуковой, свободно проходит препятствия вроде решетки с параллельными брусьями. Разумеется, при этом можно ожидать некоторого уменьшения громкости, но в других отношениях звук останется без изменения. Точно так же волны, образованные на веревке, свободно пройдут через такую решетку, если колебания частиц веревки совершаются вверх и вниз параллельно щелям между брусьями, как показано на рис. 2.1а.

Но если брусья горизонтальны, как показано на рис. 2.1b, то они остановят вертикальную поперечную волну. Здесь следует обратить особое внимание на то, что задержка волн произойдет только в том случае, если волна поперечная и колебательное движение среды перпендикулярно к щелям решетки.

Даже на таком простом примере мы видим, что продольные и поперечные волны могут распространяться существенно по - разному (вплоть до того, что поперечные волны после второго забора на рис. 2.1b не распространяются вовсе), причем это касается только поперечных волн.

В каждой точке на луче поперечной волны частицы среды колеблются перпендикулярно направлению ее распространения (волны, понятно, а не среды). Это свойство поперечной волны называется поляризацией. Давайте вспомним, что в школьном курсе геометрии утверждается, что две прямые однозначно определяют некую плоскость (кто не вспомнил, поверьте на слово: так оно и есть).