Волновое уравнение

Волновое уравнение, описывающее распространение света в веществе можно получить из уравнений Максвелла […].

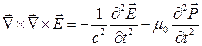(1.2)
где используется соотношение 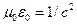, с – скорость света в вакууме, 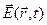– электрическое поле световой волны, 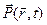– индуцированная электрическим полем поляризация среды, 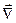- векторный дифференциальный оператор набла 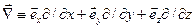, 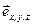- единичные вектора, направленные вдоль соответствующих осей (выражение 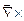означает ротор, а 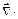означает дивергенцию),.

Вообще говоря, чтобы определить 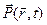, нужно использовать квантово-механическую теорию, особенно тогда, когда частота оптического поля близка к резонансным частотам среды. В прозрачных средах, т.е. вдали от резонансных частот, для связ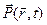и и 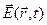можно использовать самые общие феноменологические соотношения.

По характеру функциональной зависимости 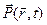от 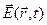можно провести классификацию материальных сред. Среды, в которых зависимость поляризации от поля является локальной и безынерционной, т.е. значение поляризации среды в некоторой точке в некоторый момент времени определяется значением поля в той же самой точке и в тот же момент, называются недиспергирующими. Нелокальность отклика приводит к пространственной дисперсии среды, а его инерционность, т.е. запаздывание поляризации относительно поля – к временной или частотной дисперсии. Линейными называются среды, в которых зависимость поляризации от поля выражается линейным оператором, в частности, линейным запаздывающим функционалом или тензорным оператором. Соответственно, нелинейными называются среды, для которых эта зависимость нелинейна. Изотропными называют среды, в которых поляризация ориентирована параллельно электрическому полю. Наконец, в анизотропных средах вектор поляризации, вообще говоря, не параллелен вектору электрического поля.

Материальные уравнения

Связь между индуцированной поляризацией 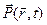и электрическим полем 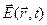определяют материальные уравнения. Для нахождения материальных уравнений, описывающих взаимосвязь 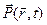с 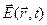необходимо воспользоваться физической моделью среды.

Материальные уравнения в прозрачных диэлектрических средах

Будем исходить из того, что отклик 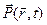прозрачного диэлектрика на световое воздействие 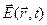в общем случае нелинейный и не мгновенный, не локальностью отклика пренебрежем. С теоретической точки зрения возникновение нелинейного отклика связано с ангармоническим движением связанных электронов и ионов при воздействии приложенного поля. В результате индуцированная поляризация 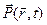электрических диполей может быть выражена в следующем виде:

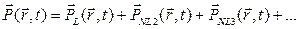(5.6)

где 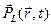линейная часть поляризации а 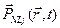– нелинейная часть поляризации 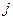-го порядка. Главный вклад в 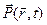вносит линейная восприимчивость, определяющая возникновение 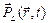. Она определяет показатель преломления 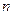и постоянную затухания 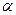. Линейная часть связана с электрическим полем следующим соотношением:

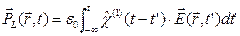(5.7)

где 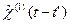– в общем случае тензор размерности 3х3.

С нелинейностью второго порядка 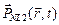связаны такие эффекты, как генерация второй гармоники и генерация суммарной частоты. Однако эта восприимчивость не равна нулю только для сред, в которых на молекулярном уровне отсутствует симметрия инверсии. Так как в кварцевых стеклах молекула SiO₂ обладает центром симметрии в оптических волокнах, обычно не наблюдаются эффекты второго порядка. Тем не менее, слабые нелинейные эффекты второго порядка могут возникать из-за электрических квадрупольных и магнитных дипольных моментов. Примеси внутри сердцевины волокна могут также при определенных условиях приводить к генерации второй гармоники. Нелинейные эффекты выше третьего порядка обычно малы, и обычно ими можно пренебречь.

При анализе распространения световых сигналов в кварцевых волокнах, таким образом, достаточно рассмотреть вклад линейной поляризации и нелинейной поляризации третьего порядка (кубичной нелинейности). В этом случае нелинейная часть связана с электрическим полем следующим соотношением:

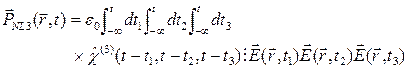(5.8)

где 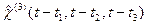– в общем случае тензор 3 ранга. Соотношения (5.7), (5.8) справедливы в дипольном приближении, когда предполагается, что отклик среды является локальным, но не мгновенными.

Ввиду сложности уравнений (5.6)-(5.8) обычно используют дополнительные упрощающие предположения. Наиболее общее упрощение состоит в том, что нелинейная поляризация 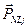в (5.6) считается малым возмущением полной индуцированной поляризации. Такое приближение оправданно, так как в оптических системах связи нелинейные эффекты относительно слабы. Более того, часто можно ограничиться рассмотрением распространения световых сигналов в линейном приближении.

Гармонические световые волны в однородной изотропной линейной среде

В материальной однородной линейной среде также как и в вакууме существуют точные решения волнового уравнения в виде гармонических волн. (Отметим, что решения в виде гармонических волн в нелинейных средах, являются приближенными, хотя в некоторых случаях такие приближенные решения очень мало отличается от точных). Решение в виде физически реальных волн может быть записано следующим образом:

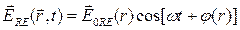, (5.9)
где 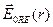– амплитуда электрического поля, 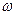– угловая частота, 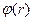– фаза электрического поля. Амплитуда и фаза электрического поля зависят от пространственной координаты 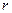. Угловая частота связана с частотой 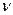и периодом 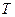выражением:

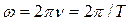(5.10)

Для описания гармонических волн удобно использовать комплексную форму, которая существенно упрощает вычисления.

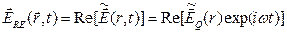, (5.11)
где 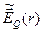– комплексная амплитуда электрического поля.

Комплексная амплитуда может быть выражена через действительную амплитуду и фазу гармонического колебания следующими двумя эквивалентными выражениями:

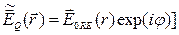, (5.12)

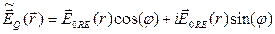, (5.13)

Подстановка выражения (5.11) для гармонической волны в уравнение (5.5) приводит к уравнению Гельмгольца для световых волн в диэлектрике:

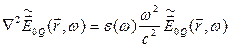(5.14)

где 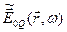– комплексная амплитуда электрического поля гармонической световой волны. Относительная диэлектрическая проницаемость, зависящая от частоты, определяется следующим образом:

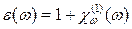, (5.15)
где 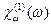--- Фурье-преобразование функции 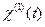. Вообще 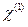, а следовательно, и 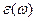- комплексные величины. По определению показатель преломления 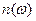и коэффициент поглощения 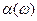связаны с действительной и мнимой частями :

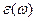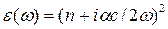. (5.16)

С помощью выражений (5.15) и (5.16) 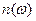и 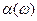можно выразить через :

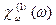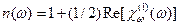(5.17)

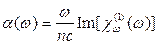(5.18)

здесь 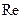и 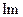обозначают соответственно действительную и мнимую части комплексного числа.

Простейшее, но очень важное решение уравнения (5.5) в однородной среде представляет собой плоскую монохроматическую волну, распространяющуюся в направлении оси :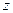

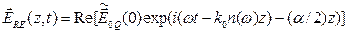, (5.19)

В отличие от плоской монохроматической волны в вакууме фазовая скорость распространения плоской монохроматической волны в материальной среде 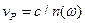зависит от частоты, а ее амплитуда уменьшается по мере распространения с коэффициентом затухания по амплитуде 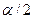(коэффициент затухания по интенсивности равен ).

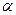Волны, распространяющиеся в однородных средах, характеризуются определенной связью между длиной волны 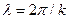и частотой волны 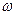. Введенный параметр 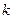называется волновым числом. Его взаимосвязь с частотой волны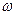

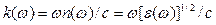, (5.20)

или обратная ей зависимость 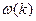называется законом дисперсии, а удовлетворяющие ей волны называются свободными или нормальными.

В прозрачных однородных средах можно пренебречь мнимой частью 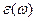( 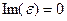). Тогда в дальнейшем 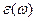можно заменить на 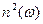, а потери можно будет включить в рассмотрение позднее, применяя метод возмущений. При таких упрощениях волновое уравнение принимает следующую форму:

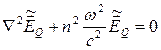, (5.21)

Для получения вида дисперсионных зависимостей 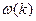надо найти явный вид функции 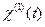или ее Фурье-образ 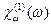. Эти две функции связаны прямым и обратным преобразованием Фурье:

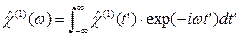(5.22)

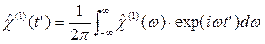(5.23)

Так как отклик среды не может опережать воздействие на нее, то 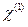(t<0)=0, а выражение (5.22) принимает вид:

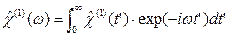(5.24)

Зависимость поляризации от поля (1.2.9) можно записать в виде

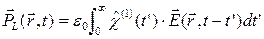(5.25)

Формула (5.25) носит название интеграла Дюамеля. Согласно этой формуле, отклик линейной системы есть линейный запаздывающий функционал относительно входного воздействия. Математически в этой формуле 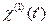– функция Грина, зависящая только от свойств среды и связанная с линейной оптической восприимчивостью среды 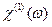формулой (5.24).

Классическая осцилляторная модель среды

В приближении линейной изотропной однородной среды ее оптическую поляризацию 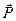, имеющую смысл дипольного момента единицы объема, можно представить в виде:

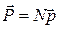(5.26)

где 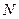– число частиц (атомов или молекул) в единице объема, а 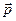– дипольный момент отдельной частицы. Частицы среды могут быть либо нейтральными, либо обладать собственным дипольным моментом. Во втором случае в изотропном веществе ориентация диполей в отсутствии внешнего поля случайная и в целом поляризация среды отсутствует. Однако, если приложено внешнее поле, то происходит либо поляризация частиц, либо поворот уже имеющихся дипольных моментов частиц под действием электрического полю, и у единицы объема появляется средний дипольный момент.

В линейном приближении дипольный момент молекулы пропорционален электрическому полю

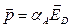, (5.27)

где 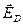– действующее на молекулу электрическое поле. В разреженном газе, содержащем 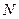частиц в единице объема, взаимодействием дипольных моментов частиц можно пренебречь ( 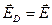) и объемная поляризация среды 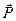определяется выражением

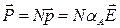(5.28)

Для газов относительная диэлектрическая проницаемость с учетом (5.28) равна:

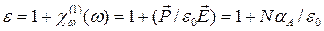. (5.29)

В случае конденсированных веществ, в частности твердых диэлектриков, необходимо учитывать влияние, оказываемое на степень поляризации каждой отдельной частицы окружающими ее частицами. При использовании простейшего приближения, которое оказывается точным для идеальной кубической решетки, полагают, что каждая поляризуемая частица представляет собой сферическую замкнутую полость в однородном диэлектрике. При этом под действием среднего (внешнего) поля 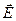локальное поле (действующее на частицу) увеличивается 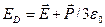. Физически это означает, что на каждую частицу конденсированного вещества действуют помимо внешнего поля 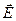еще и поля, создаваемые дипольными моментами окружающих ее частиц. Таким образом, в конденсированном веществе в соответствии с (5.27) поляризация среды определяется следующим неявным выражением:

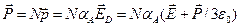. (5.30)

Из (3.30) несложно получить явное выражение для зависимости :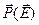

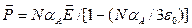. (5.31)

Таким образом, в случае твердых диэлектриков выражение для относительной диэлектрической проницаемости будет иметь вид:

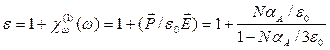. (5.32)

Этот результат иногда выражают в иной форме, предложенной Моссотти:

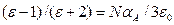. (5.33)

Из (5.33) легко выразить в явном виде зависимость поляризуемости молекулы конденсированного вещества от диэлектрической проницаемости, которая получила название формулы Лорентц-Лоренца:

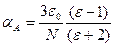. (5.34)

Рассмотрим классическую «осцилляторную» модель среды, предложенную Лоренцем. Согласно этой модели вещество состоит из нейтральных атомов, дипольный момент 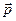которых определяется смещением 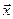электронов из состояния равновесия (относительно атомного ядра):

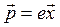(5.35)

где 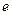– заряд электрона. При воздействии электрического поля электромагнитной волны уравнение движения электрона имеет вид:

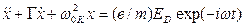, (5.36)

где 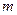– масса электрона, 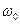– собственная частота колебаний электрона, параметр 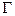– описывает затухание колебаний. Решение уравнения (5.36) имеет вид:

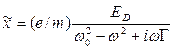, (5.37)

Поскольку 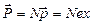для поляризации газа получаем выражение

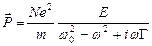(5.38)

Сравнив формулы, находим выражение для линейной оптической восприимчивости газа в модели Лоренца:

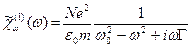(5.39)

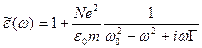(5.40)

Для разреженных газов нетрудно получить также функцию импульсного отклика подставив (5.39) в (5.23)

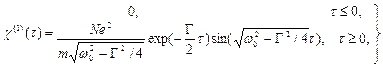(5.41)

Аналогично для конденсированного вещества с учетом (5.33) получаем следующее неявное выражение для относительного показателя преломления

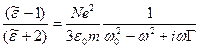. (5.42)

или следующее явное выражение, получаемое из (5.32)

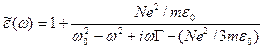(5.43)

Из (5.43) и (5.40) видно, что в случае конденсированных диэлектриков сохраняется резонансная форма зависимостей 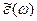и изменяется только резонансная частота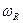

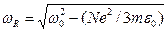, (5.44)

Если учесть все возможные резонансы и ввести коэффициенты 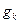, называемые силой осциллятора, получим

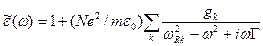(5.45)

Из формулы (5.45) следует связь между действительной и мнимой частями диэлектрической проницаемости.

Распространение световых импульсов

Световые импульсы можно рассматривать как суперпозицию плоских монохроматических световых волн с различными частотами и волновыми векторами. Ограничимся рассмотрением одномерной задачи, т.е. задачи о распространении импульса, зависящего только от одной координаты, в однородной и изотропной среде можно ограничиться скалярным вариантом теории, понимая под 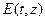какую-либо декартову компоненту поля. Пренебрежем также поглощением света средой.

Рассмотрим задачу, когда задан световой импульс 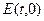в плоскости 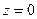и требуется установить характер эволюции этого импульса по мере распространения в пространстве, т.е. .

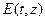Введем обозначение

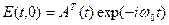(6.8)
где 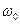– некоторая средняя частота, которую принято называть оптической несущей частотой, 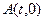– огибающая амплитуды входного светового сигнала, в общем случае комплексная функция времени. Представим 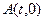в виде интеграла Фурье:

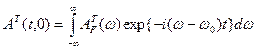(6.9)
Функция 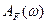есть преобразование Фурье от амплитуды входного импульса:

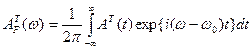(6.10)
Поскольку каждая Фурье-компонента светового импульса в линейной среде распространяется независимо от других, то мы можем сконструировать функцию 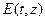в виде

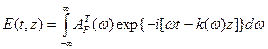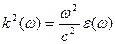, . (6.11)

Выражение (6.11) справедливо при любой спектральной плотности 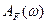и при любой зависимости волнового вектора от частоты 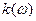, и в этом смысле оно общее и точное. Но, поскольку в данном решении пренебрегается нелинейными эффектами, то с этой точки зрения оно является приближенным.

Самый простой случай отвечает распространению импульса в вакууме:

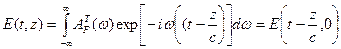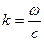, , (6.12)
т.е. сигналы (импульсы) распространяются как целое со скоростью света в вакууме и не изменяют своей формы. Это вполне понятно, т.к. гармоники распространяются с одинаковой скоростью, и между ними не возникает дополнительный набег фаз.

В реальных средах с дисперсией скорости распространения гармоник различны и между ними указанные набеги фаз возникают. Рассмотрим детальнее распространение импульса с относительно узким спектром 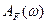и центральной частотой 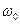. Разложим зависимость 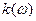в степенной ряд около 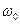и ограничимся первыми членами разложения:

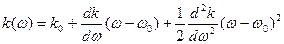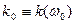, . (6.13)

Если пренебречь квадратичным членом разложения, что допустимо при выполнении условия

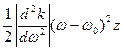<<1 (6.14)
и учесть, что согласно (6.1) 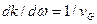, то (6.11) примет ид

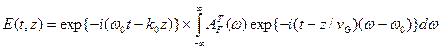. (6.15)
Сопоставляя выражения (6.15) и (6.9), можно заключить, что интеграл в (6.15) совпадает с 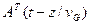и эволюция светового сигнала описывается выражением

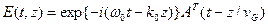. (6.16)
В рассматриваемом приближении как и в случае бигармонической волны быстро осциллирующая оптическая несущая 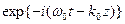распространяется с фазовой скоростью 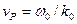. Более медленно изменяющаяся огибающая 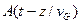сохраняет свою форму и распространяется с групповой скоростью .

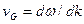Дифференцирование 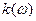по 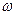приводит к формуле, связывающей групповую и фазовую скорости

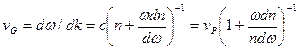. (6.17)
В области прозрачности диэлектриков и полупроводников производная показателя преломления по частоте больше 0 и 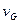< 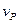, т.е. огибающая импульса отстает от несущей.

Волновое уравнение для огибающей светового импульса

Непосредственно из уравнений Максвелла можно получить уравнение, описывающее распространение световых сигналов в материальной среде. Уравнение (5.5) Лекции 5 с учетом (5.6) и равенства

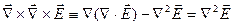(6.18)
можно записать в виде:

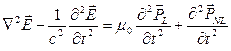(6.19)

Фурье-компоненты электрического поля удовлетворяют уравнению Гельмгольца (5.21). Из этого уравнения (в пренебрежении нелинейными эффектами и с учетом малости второй производной от медленно меняющейся огибающей) можно получить уравнение для Фурье компонент медленно меняющейся огибающей:

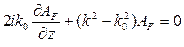(6.20)

Воспользовавшись приближенным выражением

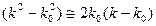(6.21)
получим следующее уравнение

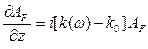(6.22)

Физический смысл этого уравнения состоит в том, что каждая спектральная компонента огибающей импульса в процессе распространения приобретает фазовый сдвиг, величина которого зависит от частоты. Воспользовавшись разложением k(ω) в ряд Тейлора (6.13) и используя обратное преобразование Фурье уравнения (6.20) получим уравнение для 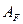во временной области. Учитывая, что операция фурье-преобразования (ω−ω₀) заменяется оператором дифференцирования i(∂/∂t), получаем

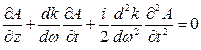. (6.23)

Для анализа эволюции световых импульсов и сигналов удобно использовать систему координат, движущуюся совместно с импульсом с групповой скоростью 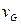(так называемые бегущие координаты). Переход к бегущим координатам осуществляется заменой переменных:

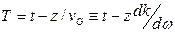(6.24)
В новых координатах уравнение (6.22) будет иметь следующий вид:

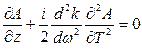. (6.25)

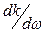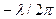Это уравнение аналогично уравнению, описывающему дифракцию световых пучков в поперечном направлении в параксиальном приближении. Дисперсионное уравнение в точности совпадает с дифракционным в одномерном случае (т.е. при распространении световых пучков в планарных волноводах) при замене на , где 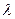– длина световой волны. В самом деле, временные эффекты, связанные с дисперсией, имеют близкие аналогии с пространственными дифракционными эффектами. Аналогия между пространственной дифракцией и временной дисперсией оказывается во многих случаях очень продуктивной.