Векторные волны

В общем случае решением уравнения Максвелла является волна, состоящая из нескольких компонент, т.е. имеющая векторный, а не скалярных характер. Рассмотрим простейшее решение системы уравнений в виде плоской волны. Каждая из компонент поля зависит от пространственных и временных переменных только через их комбинацию:

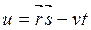, (6.26)

т.е. 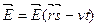(6.27)

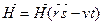(6.28)

где 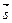- единичный вектор в направлении распространения волны

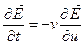(6.29)

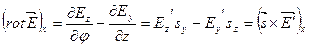. (6.30)

Уравнения Максвелла тогда примут вид:

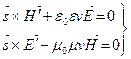. (6.31)

Считая постоянную интегрирования равной нулю, т.е. пренебрегая постоянным полем, и учитывая, что 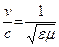, получим решения:

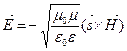; (6.32)

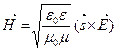. (6.33)

Умножая скалярно полученные выражения на 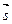, получаем условие поперечности электромагнитной волны:

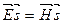. (6.34)

Оно показывает, что электрический и магнитный векторы лежат в плоскости, перпендикулярной направлению распространения.