Сложение перпендикулярных колебаний.
Пусть имеются два гармонических колебания одинаковой частоты, направления колебаний которых взаимно перпендикулярны друг другу.
            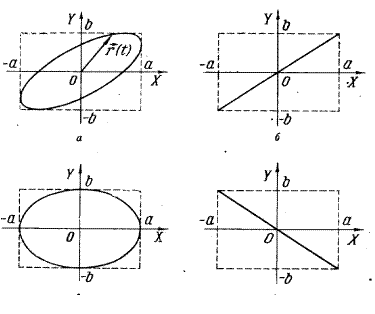 Рис.5.6
Рис.5.6
| Выберем начало отсчета времени так, чтобы начальная фаза одного из колебаний была равна нулю. При таком условии колебания можно записать так:
x = a sin wt ,
y = b sin(wt + j),
где величина j представляет разность фаз обоих колебаний. Первое уравнение можно переписать так:
 (5-7)
тогда как второе после преобразования по формуле (5-7)
тогда как второе после преобразования по формуле
|
суммы синусов двух углов принимает вид  . (5-8)
. (5-8)
Из первого уравнения следует, что
 = ±
= ±  . (5-9)
. (5-9)
Заменяя в уравнении (5-8 ) sinwt и coswt их эквивалентами из уравнений (5-7) и (5-9) , можно найти:
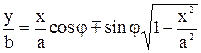 ,
,
или  (5-10)
(5-10)
Возводя обе части уравнения (5-10) в квадрат и учитывая, что sin2 j + cos2 j = 1, получим:
 . (5-11)
. (5-11)
Уравнение (5-11) является уравнением эллипса, оси которого повернуты относительно осей координат (рис.5.6а)). При sinj = 0 и sinj = p эллипс вырождается в прямую (рис.5.6 в) и д) )
 . (5-12)
. (5-12)
При разности фаз между колебаниями p2 оси эллипса совпадают с осями
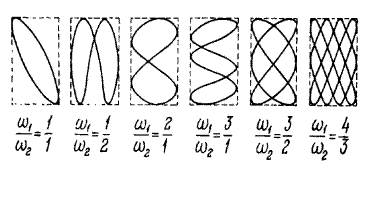 Рис.5.7 Рис.5.7
| координат (рис.5.6в). Если частоты складываемых колебаний отличаются друг от друга, то форма кривой, которую описывает радиус-вектор суммарного колебания, становится очень сложной и зависит от соотношения складываемых частот. Для некоторых соотношений частот складываемых колебаний получающиеся фигуры, называемые фигурами Лиссажу,показаны на рис.5.7. |
Дата добавления: 2015-04-15; просмотров: 1040;
