Вращательное движение твердого тела.

Вращательным называется такое движение твердого тела, при котором точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения тела, и описывает окружности, центры которых лежат на этой оси.

АВ – ось вращения,

Р – неподвижная плоскость,

Q – подвижная плоскость,

Двухгранный угол 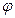– угол поворота тела.

Угол поворота будем считать положительным, если смотреть навстречу оси вращения и видеть его направления против часовой стрелки. Численное значение угла поворота выражается в радианах: [ 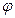] = рад.

Рис. 2.9

Угол поворота (в радианах) часто выражают через число оборотов N:

.

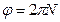Угол 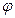, определяя положение подвижной полуплоскости, определяют также положение всего вращающегося тела. Поэтому его можно рассматривать как угловую координату тела.

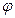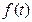= (18)

Выражение (18) является уравнением вращательного движения твердого тела.

Главными кинематическими характеристиками вращательного движения твердого тела в целом является угловая скорость – 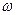и угловое ускорение – .

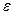Пусть в момент времени 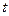движение подвижной полуоси определяется углом 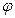, а в момент 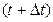– углом .

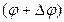Предел отношения приращения угла к приращению времени при стремлении последнего к нулю, называется угловой скоростью тела в данный момент времени:

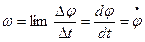(19)

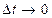
Размерность [ ] – .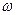

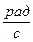В технике часто при равномерном вращении используется числом оборотов в минуту – .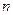

Зависимость между 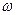и 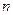имеет вид:

.

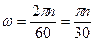Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением

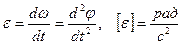. (20)

Весьма полезным является введение в рассмотрении вектора угловой скорости и вектора углового ускорения.

Вектором угловой скорости будем называть вектор, модуль которого равен абсолютному значению производной угла поворота тела по времени, направленной вдоль оси вращения в ту сторону, откуда вращение тела видно происходит против часовой стрелки.

,

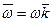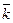– единичный орт оси z.

Вектором углового ускорения будем называть вектор, равной производной по времени от вектора угловой скорости.

.

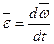Вектор 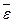как и вектор 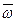– направлен вдоль оси вращения твердого тела.