Рівняння руху ідеальної нестисненої рідини

Сили, які діють в рідині, зазвичай поділяють на об’ємні (масові) та поверхневі. Об’ємні сили виникають тоді, коли зовнішні поля діють безпосередньо на частинки рідини (на атоми і молекули). Наприклад, це можуть бути сили тяжіння, інерції. Поверхневі сили виникають в результаті взаємодії молекул даної рідини з найближчими сусідніми молекулами цієї ж рідини або оточуючих тіл. Поверхневі сили – це сили, дії яких зазнає поверхня кожного об’єму з боку навколишніх частин рідини.

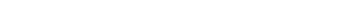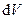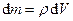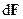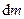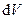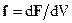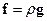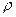Розглянемо елемент об’єму ідеальної нестисненої рідини (рис.8.1). Маса елемента . Очевидно, об’ємна сила, , що діє на цей елемент, пропорційна його масі , а значить і об’єму . Об’ємні сили зручно характеризувати величиною об’ємної густини сили, , яка дорівнює силі, що діє на одиницю об’єму рідини. Наприклад, для сили тяжіння , де – густина рідини, 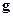– прискорення вільного падіння. Отже, об’ємна сила, що діє на елемент об’єму 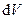(рис.8.1), дорівнює .

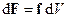Розглянемо сили, що діють на елемент об’єму рідини 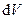(рис.8.1) в напрямку вісі OX. Об’ємну силу позначимо 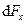, а x-компоненту поверхневих сил представимо як 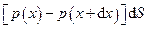, де 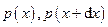- значення тиску на протилежних бічних поверхнях елемента об’єму, 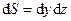- площа поверхні.

Запишемо рівняння руху (другий закон Ньютона) елемента об’єму рідини 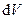у проекції на вісь OX

.

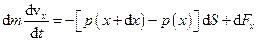Різницю тисків представимо через похідну по координаті

,

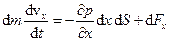Повністю аналогічні міркування для напрямків OY і OZ дозволяють записати інші два рівняння

,

.

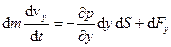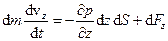Отже, ми отримали рівняння руху елемента об’єму рідини 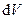у трьох проекціях на осі координат. Об’єднаємо ці три рівняння в одне векторне рівняння. Для цього помножимо їх відповідно на орти 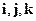і додамо праві і ліві частини. Потім розділимо на 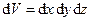, врахуємо 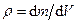, і отримаємо

,

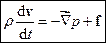де 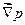- градієнт тиску - вектор, який у декартових координатах має вигляд 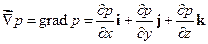. Отримане рівняння називається рівнянням Ейлера, воно є основним рівнянням динаміки ідеальної нестисненої рідини.

З рівняння Ейлера легко отримати основне рівняння гідростатики нестисненої рідини

.

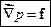Тут враховано, що в умовах статики будь-які механічні рухи відсутні, отже похідна від швидкості в рівнянні Ейлера покладена рівною нулю. З основного рівняння гідростатики випливає, що за умови рівноваги густина сили 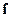повинна виражатися градієнтом певної скалярної функції, що з іншого боку є умовою того, щоб сила 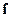була консервативною. Таким чином, для рівноваги рідини необхідно, щоб поле, в якому вона перебуває, було консервативним. В супротивному випадку рівновага рідини неможлива.