Вимушені коливання в лінійних системах при гармонійній обурюючий силі
Розглянемо лінійну систему з урахуванням опору під дією гармонійної обурючої сили. Диференціальне рівняння руху в узагальнених координатах має вигляд
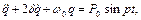 (3.1)
(3.1)
де для механічних систем, наприклад, 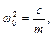
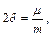
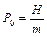 , а для електричного контуру:
, а для електричного контуру: 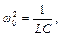
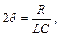
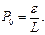
Загальне рішення рівняння (3.1) має вигляд
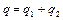 ,
,
де 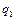 при
при 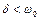 відомо (див. 2.3), а
відомо (див. 2.3), а 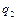 – якесь приватне рішення рівняння (3.1). Будемо шукати його у вигляді
– якесь приватне рішення рівняння (3.1). Будемо шукати його у вигляді
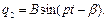
Стандартна процедура визначення постійних 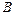 та
та 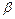 дає
дає
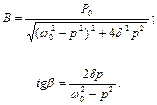 (3.2)
(3.2)
Таким чином, рішення рівняння (3.1) приймає вигляд:
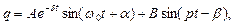 (3.3)
(3.3)
де 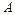 і
і 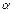 визначаєюься за початковими умовами.
визначаєюься за початковими умовами.
При 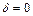 рішення (3.3) описує рух коливальної системи за відсутності опору.
рішення (3.3) описує рух коливальної системи за відсутності опору.
Розглянуті коливання є складними і складаються з власних (перший доданок в (3.3)) і вимушених коливань (другий доданок). Власні коливання після закінчення часу практично згасають і система буде робити коливання за законом
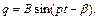
Ці коливання і називаються вимушеними. Величина 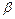 характеризує зсув фази вимушених коливань по відношенню до фази вимушених коливань.
характеризує зсув фази вимушених коливань по відношенню до фази вимушених коливань.
Для дослідження отриманих результатів введемо позначення:
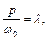
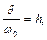
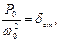
де 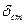 – величина статичного «відхилення» системи під дією «сили»
– величина статичного «відхилення» системи під дією «сили» 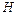 . Тоді з рівності (3.2) отримаємо
. Тоді з рівності (3.2) отримаємо
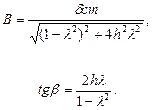 (3.4)
(3.4)
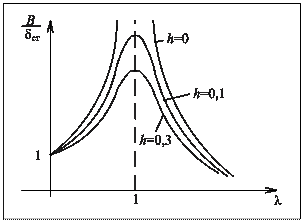
Рисунок 3.4 – Залежності коефіцієнта динамічності від співвідношення частот
Величину 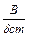 називають коефіцієнтом динамічності системи. Залежність коефіцієнта динамічності від співвідношення частот показана на рис.3.4 для різних значень
називають коефіцієнтом динамічності системи. Залежність коефіцієнта динамічності від співвідношення частот показана на рис.3.4 для різних значень 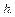
З (3.4) видно, якщо 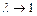 амплітуди вимушених коливань досягають максимуму. Таке явище називається резонансом. Максимуми кривих
амплітуди вимушених коливань досягають максимуму. Таке явище називається резонансом. Максимуми кривих 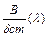 лише незначно зміщуються вліво від значення
лише незначно зміщуються вліво від значення 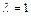 ; резонансне значення коефіцієнта динамічності часто називають добротністю системи.
; резонансне значення коефіцієнта динамічності часто називають добротністю системи.
Відзначимо, що однією з основних властивостей вимушених коливань є наступне: навіть при малій обурюючий силі можна отримати інтенсивне вимушене коливання, і навіть при великих значеннях обурючої сили вимушені коливання можна зробити як завгодно малими.
Вимушені коливання і, зокрема, резонанс відіграють велику роль у багатьох галузях фізики і техніки: амортизуючі коливальні пристрої, що реєструють прилади, помножувачі частот і т.п.
Дата добавления: 2015-06-12; просмотров: 1022;
