Додавання гармонічних коливань

Коливання, для котрих зміщення як функція часу може бути описано будь-яким законом, окрім синуса чи косинуса, називають складними (негармонічними).

Відомо, що будь-яке складне коливання можна подати у вигляді суми простих гармонічних коливань. Перш ніж аналізувати складні коливання (а таку задачу медикам дово­диться розв'язувати досить часто), розглянемо, до яких ре­зультатів може призвести додавання гармонічних коливань.

1. Додавання гармонічних коливань, спрямованих вздовж однієї прямої

Нехай тіло бере участь одночасно у двох коливаннях, спрямованих вздовж однієї прямої, причому амплітуди і періоди (частоти) цих коливань однакові, а початкові фази різні

.

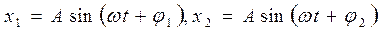Результуюче зміщення х тіла від положення рівноваги до­рівнює алгебраїчній сумі зміщень х₁ і х₂:

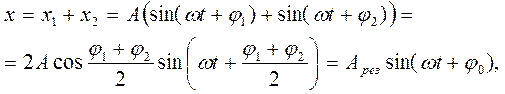де

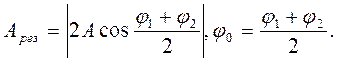
Таким чином, результуюче коливання являє собою гармонічне коливання, яке відбувається вздовж тієї ж самої прямої, що і складові коливання, і з періодом (частотою), який дорівнює періоду (частоті) складових коливань. Амплітуда результуючого коливання залежить від різниці початкових фаз складових коливань. Якщо φ₁ -φ₂ = 2kπ , де k= 0, 1,2, ...,то 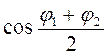= ±1 і А_рез = 2А (або А_рез = А₁+A₂, якщо A₁≠ А₂). Якщо φ₁- φ₂ = (2k + 1)π, то

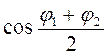= 0 і А_рез= 0 (або А_рез = А₁-A₂, якщо A₁≠ А₂ ).

Якщо складові коливання відрізняються періодами (часто­тами), то результуюче коливання вже не буде гармонічним. Розглянемо, як особливо цікавий, результат додавання двох гармонічних коливань рівних амплітуд і фаз, періоди (частоти) яких відрізняються, тобто

.

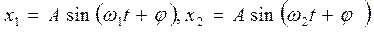Результуюче зміщення дорівнює

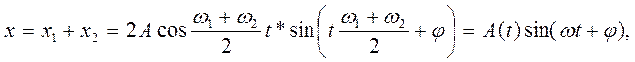
де .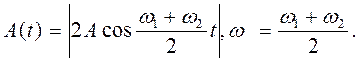

Якщо різниця ω₁-ω₂ мала, то амплітуда A(t) змінюється з часом за гармонічним законом, але з частотою 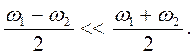Такі коливання називають биттям (мал. 1.27).

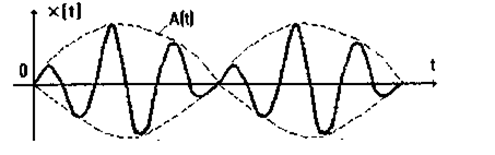
Мал. 1.27. Биття.

Період зміни амплітуди коливань називають періодом биття (Т_б). Період биття може бути визначений з умови:

.

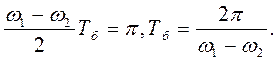Отже, частота 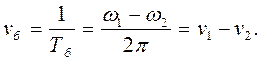. Таким чином,

частота зміни амплітуди результуючого коливання дорівнює різниці частот складових коливань.

2. Додавання взаємноперпендикулярних гармонічних коливань

Нехай матеріальна точка водночас бере участь у двох коливаннях, що відбуваються у взаємно перпендикулярних напрямках:

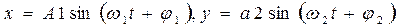
Сукупність координат х і у матеріальної точки у різні моменти часу визначають траєкторію руху матеріальної

точки у площині XY. Форма траєкторії залежить від співвід­ношення частот і різниці фаз складових коливань. Наведемо деякі випадки додавання коливань (мал. 1.28):

1) ,

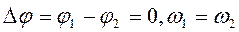рівняння траєкторії ;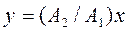

2) ,

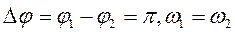рівняння траєкторії ;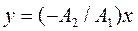

3) 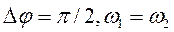, рівняння траєкторії ;

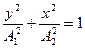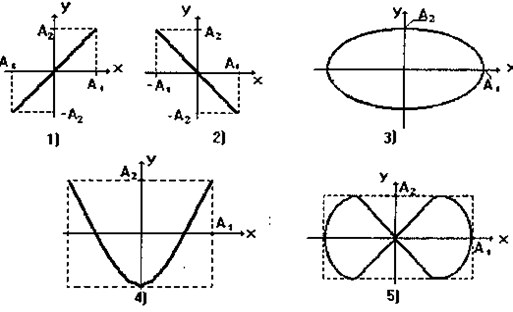
4, 5) 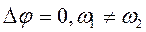, у цьому випадку форма траєкторії залежить від співвідношення частот ω₁ і ω₂. На мал. 1.28 наве­дено траєкторії для випадків ω₁:ω₂=1:2 і ω₁: ω₂= 2:3.

с

Мал. 1.28. Складання взаємно перпендикулярних коливань (фігури Лісажу).

Отримані криві, що їх описує матеріальна точка, називають фігурами Лісажу. Криві, подібні до кривих Лісажу, спостерігають при дослідженні біопотенціалів серця методом векторелектрокардіографії.