Затухаючі коливання і аперіодичний рух

Припустимо, що в розглянутих системах існує тертя чи опір, причому сила тертя (опору) пропорційна швидкості: F_m=-rυ, де r - коефіцієнт тертя (опору). Запишемо в цьому випадку рівняння руху (II закон Ньютона).

ma = -kx-rυ або .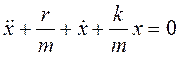

Позначивши 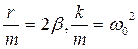,отримаємо диференційне рівняння другого порядку, що описує рух пружинного маят­ника у присутності сил тертя

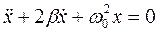. (1.49)

Складемо характеристичне рівняння, що відповідає ди-ференційному рівнянню (1.49):

.

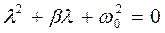Знайдемо корені характеристичного рівняння

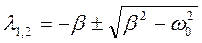. (1.50)

Загальний розв'язок рівняння (1.49) залежить від знака різниці β²-ω₀². Розглянемо всі можливі випадки:

1. β²<ω₀², коли корені характеристичного рівняння є комплексними числами (затухаючі коливання)

,

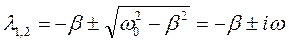де 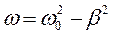- циклічна частота. У випадку комплекс­них коренів характеристичного рівняння загальний розв'я­зок (1.49) має вигляд

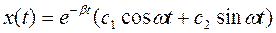, або

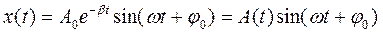, (1.51)

де A(t) = A₀e ^-βt- амплітуда коливань, яка зменшується за експоненціальним законом, (β - коефіцієнт затухання, визначає швидкість затухання амплітуди. Залежність х = f (t) для затухаючих коливань подано на мал. 1.23.

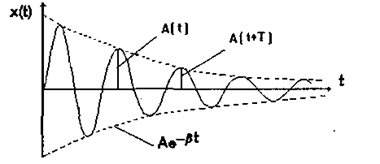
Мал. 1.23. Затухаючі коливання.

Ступінь затухання часто характеризують декрементом затухання S і логарифмічним декрементом затухання λ*:

,

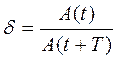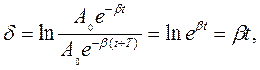
де період затухаючих коливань дорівнює

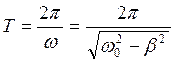
2. β²>ω₀² , коли корені характеристичного рівняння є дійсними числами (аперіодичні коливання)

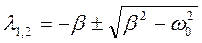<0

У цьому випадку загальний розв'язок рівняння (1.49) ма­тиме вигляд

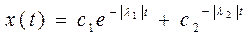(1.52)

що відповідає аперіодичному рухові (мал. 1.24).

3. β²>ω₀² , коли корені є кратними. Легко побачити, що і в цьому випадку рух тіла буде аперіодичним.

Коливання, що виника­ють у системі при відсут­ності зовнішніх сил, нази­вають вільними. Частота вільних коливань залежить як від пружних власти­востей системи (ω₀), так і від інтенсивності втрат (β). Якщо β²<<ω₀², то ω 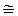ω₀ i період вільних коливань

стає близьким до періоду власних коливань (мал. 1.23).

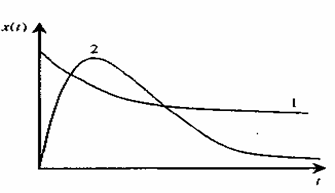
Мал. 1.24. Аперіодичний рух.