Критерії механічної подібності рідин, що рухаються

Незважаючи на різноманітність руху рідин у природі, можна поставити питання: яким умовам повинні відповідати параметри потоку і параметри рідин (густина, в'язкість тощо), щоб рухи рідин були механічно подібні? Якщо подібність має місце, то, знаючи картину плину рідини в одній системі, можна передбачити і характер плину рідини в іншій, геометричне подібній системі. Це має важливе значення не лише у техніці (випробування моделей літаків, кораблів тощо), айв експериментальній медицині (наприклад, при дослідженні процесів обтікання кров'ю різних моделей серцевих клапанів, особливостей плину рідин по штучних судинах, криволінійному ложеві насоса апарату штучного кровообігу тощо).

Розглядаючи будь-який плин рідин і рівняння його руху, можна виділити деякі важливі параметри рідини (η -в'язкість, ρ — густина, χ -модуль об'ємної пружності) і характеристики її руху (υ - швидкість, L - характерні розмі­ри, τ - деякий характерний час, протягом якого відбувають­ся помітні зміни плину тощо). У гідродинаміці відомі декілька безрозмірних величин, що являють собою комбіна­цію цих параметрів. Це числа Рейнольдса (Re), Фруда (F), Маха (М), Струхаля (S). Кожне з цих чисел має певний фізичний зміст. Так, число Маха є відношенням швидкостей руху тіла і звука у даному середовищі (М= υ/c). Число Струхаля - відношення деякого характерного розміру потоку рідини і розмірів тіла (S = υ*τ/L). Число Фруда (Ф = υ²lgL) визначає відношення кінетичної енергії рідин до її приросту, обумовленого роботою сили тяжіння на деякій характерній відстані (чим більше число Фруда, тим більша роль інерції у порівнянні з дією сили тяжіння).

Одним з найважливіших критеріїв подібності є число Рейнольдса. За порядком величини воно дорівнює відно­шенню кінетичної енергії рідини до витрати її, обумовленої роботою сил в'язкого тертя на характерній довжині. Дійсно, кінетична енергія рідини Е_к ~ ρL³υ², робота сил в'язкості А = = F_m*L. Силу в'язкого тертя знайдемо за

формулою Ньютона F_m ~ 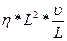. Відношення кінетичної енергії Е_к до роботи А і становить число Рейнольдса:

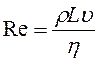(1.30)

Число Рейнольдса, таким чином, визначає відносну роль інерції і в'язкості рідини при її плині. При великих числах Рейнольдса головну роль відіграє інерція, при малих - в'язкість. При плині рідини по циліндричних трубках у ролі характерного розміру L часто використовують радіус чи діаметр судини. Потоки рідин вважаються подібними, якщо для них числа Рейнольдса і Фруда збігаються. При малих числах Рейнольдса плин в'язких рідин є ламінарним, при зростанні швидкості ламінарний плин стає нестійким і перетворюється в турбулентний. Турбулентний плин - це такий плин, гідродинамічні характеристики якого (швид­кість, тиск) різко та нерегулярно змінюються з часом і у просторі. Частинки рідини рухаються по складних траєкто­ріях, рідина інтенсивно перемішується. Прикладом такого

руху є рух крові при її вигнанні з шлуночків серця, її плині по аорті тощо.

Слід зауважити, що при турбулентному русі рідини не діють звичайні формули гідродинаміки (гемодинаміки). Так, на відміну від закону Гагена-Пуазейля і формули Пуазейля, згідно з якими при ламінарному плині об'ємна швидкість Q чи лінійна швидкість v пропорційні різниці тисків υ ~ ~ Р₁-Р₂ У першому степені, при турбулентній течії рідини за певними умовами має місце закон Шезі, згідно з яким лінійна швидкість υ~ 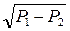. Для рідини, що тече по певній судині, можна визначити значення швидкості υ_кp, при якій рух із ламінарного перетворюється у турбулентний. Число Рейнольдса, при якому відбувається це явище, зветься критичним:

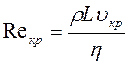. (1.31)

У геометричне подібних системах перехід від ламінар­ного до турбулентного плину відбувається завжди при од­них і тих самих значеннях числа Рейнольдса. Так, згідно (1.31) критичне значення числа Re для в'язкої рідини, що тече по довгій циліндричній трубці, становить 2300. Значення чисел Рейнольдса для крові в різних ділянках судинного русла подані у табл. 1.2.

Зауважимо, що зміна величини в'язкості крові (напри­клад, при анемії) може діагностуватися завдяки виникненню турбулентних шумів. Це пояснюється тим фактом, що при анемії коефіцієнт в'язкості зменшується у 2-3 і більше разів. Відповідно число Рейнольдса збільшується, оскільки Re ~ 1/η\. Як наслідок, число Рейнольдса стає більшим за своє критичне значення і виникає перехід від ламінарного плину крові до турбулентного.

Ще одне медичне застосування переходу між ламінар­ною і турбулентною течією крові пов'язане з вимірюванням кров'яного тиску методом Короткова. У цьому методі сис­толічний (верхній) тиск вимірюється у момент, коли кров починає протискуватися через отвір в артерії, стиснутій за допомогою манжети. Саме у цей момент виникають шуми, обумовлені появою турбулентної течії крові. Діастолічний (нижній) тиск фіксується у момент, коли ці шуми зникають внаслідок послаблення манжети і переходу течії від ламі­нарної до турбулентної.