Рівняння плоскої хвилі
Хвиля – це процес розповсюдження коливань. Якщо в якійсь точці простору збуджується коливання, то воно буде розповсюджуватись завдяки силам взаємодії, що існують між частинками середовища. В залежності від напрямку коливань частинок середовища по відношенню до напрямку розповсюдження хвилі бувають повздовжні (в газах, рідинах і твердих тілах) і поперечні (виникають, коли є пружні сили відносно зсуву).
 Щоб описати хвилю треба вказати як буде залежати зміщення
Щоб описати хвилю треба вказати як буде залежати зміщення  від просторової координати і часу, тобто знайти
від просторової координати і часу, тобто знайти  . У випадку одномірного розповсюдження хвилі, наприклад, вздовж осі
. У випадку одномірного розповсюдження хвилі, наприклад, вздовж осі 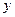 (рис.97) коливання частинок, що знаходяться в певній площині
(рис.97) коливання частинок, що знаходяться в певній площині 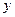 будуть запізнюватися на час
будуть запізнюватися на час 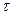 порівняно з коливаннями у точці
порівняно з коливаннями у точці 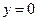 .
.
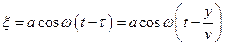
де 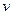 – швидкість розповсюдження збурення. Аргумент косинуса
– швидкість розповсюдження збурення. Аргумент косинуса 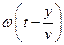 називається фазою хвилі.
називається фазою хвилі.
Геометричне місце точок, до яких доходить коливання в момент часу 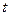 , називається фронтом хвилі. Хвильова поверхня – це геометричне місце точок однакової фази. Хвильові поверхні можуть бути складні, в найпростіших випадках вони мають форму площини або сфери, тому говорять про плоску або сферичну хвилю.
, називається фронтом хвилі. Хвильова поверхня – це геометричне місце точок однакової фази. Хвильові поверхні можуть бути складні, в найпростіших випадках вони мають форму площини або сфери, тому говорять про плоску або сферичну хвилю.
Довжина хвилі 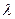 – найменша відстань між точками простору, які мають однакове зміщення, або що відрізняються по фазі на величину
– найменша відстань між точками простору, які мають однакове зміщення, або що відрізняються по фазі на величину 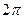 , як це вимагає періодичність косинуса. З означення
, як це вимагає періодичність косинуса. З означення 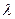 випливає
випливає
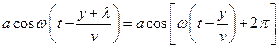 ,
,
звідки 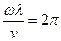 або
або 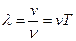 . З останнього співвідношення випливає інше означення
. З останнього співвідношення випливає інше означення 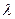 , як відстані, на яку поширюється хвиля за час, рівний періоду коливань частинок середовища.
, як відстані, на яку поширюється хвиля за час, рівний періоду коливань частинок середовища.
Таким чином, рівняння плоскої хвилі (і повздовжньої, і поперечної), яка розповсюджується вздовж осі 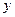 , можна представити у вигляді
, можна представити у вигляді
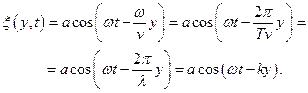
Тут введено величину  , яка називається хвильовим числом.
, яка називається хвильовим числом.
Якщо зафіксувати якусь фазу 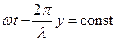 , і взяти похідну по часу від цього виразу, то можна знайти величину швидкості
, і взяти похідну по часу від цього виразу, то можна знайти величину швидкості
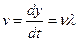 ,
,
яка одночасно є швидкістю пересування фази і називається фазовою швидкістю.
Згідно 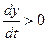 , тому рівняння описує хвилю, яка розповсюджується в додатному напрямку осі
, тому рівняння описує хвилю, яка розповсюджується в додатному напрямку осі 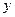 . Хвиля, яка розповсюджується в протилежному напрямку (для неї
. Хвиля, яка розповсюджується в протилежному напрямку (для неї  ) описується рівнянням
) описується рівнянням
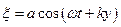 .
.
 Знайдемо рівняння плоскої хвилі, яка розповсюджується у напрямку, що визначається напрямляючими косинусами
Знайдемо рівняння плоскої хвилі, яка розповсюджується у напрямку, що визначається напрямляючими косинусами 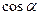 ,
, 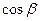 ,
, 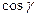 , де
, де 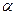 ,
, 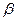 ,
, 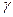 - кути, які утворює з осями
- кути, які утворює з осями 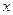 ,
, 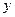 ,
, 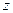 нормаль до фронту плоскої хвилі (рис.98). Нехай плоска хвильова поверхня знаходиться на відстані
нормаль до фронту плоскої хвилі (рис.98). Нехай плоска хвильова поверхня знаходиться на відстані 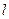 від початку координат. Тоді коливання в цій площині будуть запізнюватись на час
від початку координат. Тоді коливання в цій площині будуть запізнюватись на час 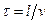 від коливань в площині, що проходить через початок координат, і будуть описуватись рівнянням
від коливань в площині, що проходить через початок координат, і будуть описуватись рівнянням
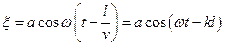 ,
,
де 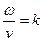 – модуль хвильового числа.
– модуль хвильового числа.
Якщо 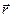 – радіус-вектор довільної точки хвильової поверхні, тоді
– радіус-вектор довільної точки хвильової поверхні, тоді
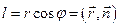 ,
,
де  – одиничний вектор нормалі до хвильової поверхні.
– одиничний вектор нормалі до хвильової поверхні.
Введемо хвильовий вектор 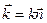 . Проекції хвильового вектора на координатні осі дорівнюють
. Проекції хвильового вектора на координатні осі дорівнюють
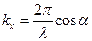 ,
, 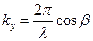 ,
, 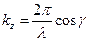 .
.
Замінивши в величину 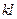 скалярним добутком
скалярним добутком 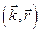 [оскільки
[оскільки 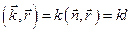 ], одержимо рівняння хвилі
], одержимо рівняння хвилі
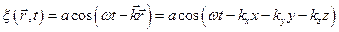 .
.
Дата добавления: 2015-06-17; просмотров: 1094;
