Хвильове рівняння. Рівняння любої хвилі є розв’язком диференціального рівняння, яке називається хвильовим

Рівняння любої хвилі є розв’язком диференціального рівняння, яке називається хвильовим. Щоб встановити вигляд хвильового рівняння, співставимо другі часткові похідні по координатам і по часу від функції . Продиференціювавши цю функцію маємо

,

,

,

.

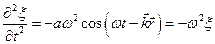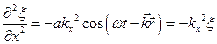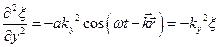Складання похідних по координатам дає

.

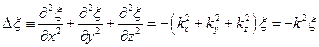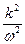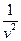Співставивши цю суму з похідною по часу і замінивши на , одержимо співвідношення

.

Це і є хвильове рівняння.

Легко впевнитись, що хвильовому рівнянню задовольняє не тільки рівняння , а і люба функція типу

.

Підставляючи її в хвильове рівняння одержимо тотожність при умові .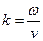

Для плоскої хвилі, що розповсюджується уздовж осі 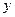хвильове рівняння має вигляд

.

Як показують розрахунки швидкості пружніх хвиль в твердих тілах, швидкість повздовжніх хвиль дорівнює кореню квадратному від модуля Юнга 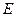, поділеного на густину середовища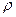

,

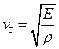а швидкість поперечних хвиль визначається співвідношенням

,

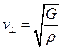де 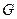– модуль зсуву.