Інтерференція хвиль

Якщо в середовищі розповсюджуються декілька хвиль, то результуюче коливання частинок середовища є сумою коливань, які виконували б частинки при розповсюдженні кожної хвилі окремо. Це твердження базується на дослідних фактах і носить назву принципу суперпозиції (накладання) хвиль.

Якщо коливання в кожній точці середовища, під впливом кожної із хвиль, відбуваються з сталою різницею фаз, то такі хвилі називаються когерентними. При складанні когерентних хвиль виникає явище інтерференції, яке полягає в тому, що результуючі коливання в деяких точках простору підсилюються, а в інших послаблюються. Окремим випадком інтерференції хвиль є стояча хвиля, яка утворюється при складанні двох хвиль з однаковими амплітудами, які поширюються назустріч одна одній. В дійсності стоячі хвилі виникають при відбиванні хвиль від перешкод.

Запишемо рівняння двох плоских хвиль, що розповсюджуються в протилежних напрямках вздовж осі . Вибором початку відліку координати і часу спростимо рівняння так, щоб початкові фази в них були рівні нулю. Отже, маємо

,

.

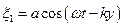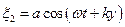Склавши ці рівняння з врахуванням перетворень для суми косинусів, одержимо

.

З видно, що в кожній точці стоячої хвилі відбувається коливання з частотою 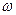і амплітудою, яка залежить від :

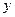амплітуда .

В точках, координати яких задовольняють умові

,

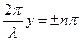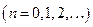
коливання відбуватимуться з максимальною амплітудою. Ці точки називаються пучностями. Координати пучностей одержуємо з

.

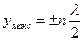Ті точки простору, в яких амплітуда коливань дорівнює нулю, визначаються умовою

, .

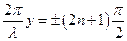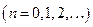Ці точки називаються вузлами стоячої хвилі. Координати вузлів з дорівнюють

.

На рис.99 приведений графік розподілу зміщень частинок з положення рівноваги в стоячій хвилі вздовж просторової координати 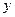для двох 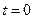і 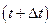моментів часу. Пунктиром показаний розподіл зміщень через пів періоду, тобто для моменту часу .

Розглянемо інтерференцію хвиль від двох точкових джерел 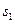і 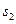(рис.100). Коливання в довільній точці 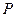, яка розташована на відстані 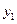від 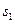і відстані 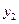від 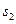, описуються рівняннями

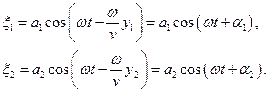
Тут введені позначення

, .

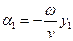Застосовуючи графічний спосіб складання коливань 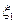і 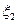можна відразу записати амплітуду результуючого гармонічного коливання, яка згідно матиме вигляд

,

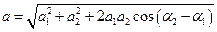де 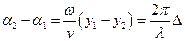. Тут 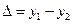– різниця ходу.

При різниці фаз 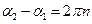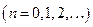, що відповідає різниці ходу 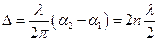, амплітуда коливань буде максимальною 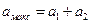. В цих точках простору спостерігатиметься підсилення коливань.

При різниці фаз 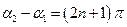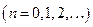, що відповідає різниці ходу 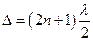, амплітуда коливань буде мінімальною 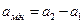. В точках, для яких різниця ходу кратна непарній кількості половинок довжин хвиль, буде спостерігатися послаблення коливань.