Гармонічні коливання. Розглянемо коливання, які описуються рівнянням
Розглянемо коливання, які описуються рівнянням
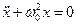 .
.
Розв’язок шукатимемо у вигляді підстановки
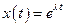 ,
,
де 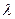 – стала величина. Після диференціювання
– стала величина. Після диференціювання
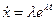 ,
, 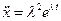
і підстановки в , отримаємо характеристичне рівняння
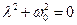 ,
,
корні якого дорівнюють
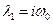 ,
, 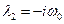 .
.
Згідно загальний розв’язок рівняння має вигляд
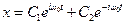 .
.
Функція, яка описує реальний фізичний процес, в даному випадку коливання, має бути дійсною. Використаємо умову дійсності комплексного числа 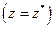 для знаходження коефіцієнтів
для знаходження коефіцієнтів 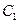 і
і 
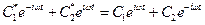 .
.
Рівність матиме місце за умовою рівних коефіцієнтів при однакових степеневих функціях, тобто
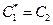 ,
, 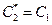 .
.
Запишемо коефіцієнти 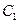 і
і  в показниковій формі
в показниковій формі
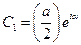 ,
, 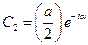 .
.
Тут 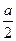 – модуль і
– модуль і 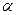 – аргумент комплексного числа. Підстановкою цих виразів в , одержимо
– аргумент комплексного числа. Підстановкою цих виразів в , одержимо
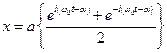 ,
,
а з врахуванням формули , маємо розв’язок рівняння
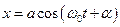 .
.
Тут 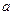 і
і 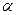 – сталі величини.
– сталі величини.
Графік функції , яка визначає гармонічне коливання, представлений на рис.88.
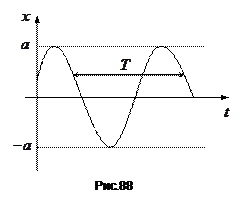 Зміщення
Зміщення  змінюється з часом за законом косинуса. Величина найбільшого відхилення кульки від положення рівноваги називається амплітудою
змінюється з часом за законом косинуса. Величина найбільшого відхилення кульки від положення рівноваги називається амплітудою 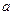 . Величина
. Величина 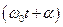 називається фазою коливання, а
називається фазою коливання, а 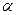 – початковою фазою.
– початковою фазою.
Оскільки косинус – періодична функція з періодом 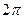 , назвемо періодом
, назвемо періодом 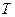 той інтервал часу, за який фаза коливання отримає приріст, рівний
той інтервал часу, за який фаза коливання отримає приріст, рівний 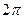 . Тоді період визначатиметься співвідношенням
. Тоді період визначатиметься співвідношенням
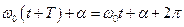 ,
,
звідки
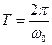 .
.
Кількість коливань за одиницю часу називається частотою коливання 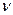 . Очевидно, з періодом частота пов’язана співвідношенням
. Очевидно, з періодом частота пов’язана співвідношенням 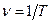 . Тоді з маємо
. Тоді з маємо
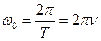 .
.
Тут 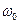 – циклічна частота, яка визначає кількість коливань за
– циклічна частота, яка визначає кількість коливань за 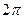 секунд.
секунд.
Кожне конкретне коливання характеризується своєю амплітудою 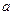 і початковою фазою
і початковою фазою 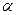 , величини яких визначаються початковими умовами, тобто значеннями відхилення
, величини яких визначаються початковими умовами, тобто значеннями відхилення 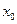 і швидкості
і швидкості 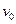 в початковий момент часу. Спочатку диференціюванням виразу отримаємо швидкість
в початковий момент часу. Спочатку диференціюванням виразу отримаємо швидкість
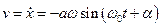 .
.
Поклавши в рівняннях і 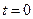 , маємо два рівняння
, маємо два рівняння
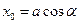 ,
,
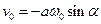 ,
,
з яких дійсно можна отримати 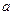 і
і 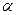 :
:
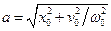 ,
,
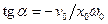 .
.
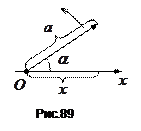 Складання гармонічних коливань одного напрямку
Складання гармонічних коливань одного напрямку
Тобто складання гармонічних функцій, часто спрощується за рахунок застосування графічного способу складання векторів на площині. В цьому способі коливання представляють у вигляді вектора 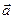 , який обертається навколо точки
, який обертається навколо точки 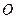 , що належить осі
, що належить осі  , з кутовою швидкістю
, з кутовою швидкістю 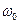 (рис.89).
(рис.89).
Якщо напрям вектора 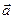 утворює з віссю
утворює з віссю  кут
кут 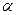 в початковий момент часу
в початковий момент часу 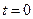 , то проекція вектора
, то проекція вектора 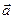 на вісь
на вісь  -ів буде змінюватись з часом за законом гармонічних коливань
-ів буде змінюватись з часом за законом гармонічних коливань
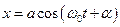 .
.
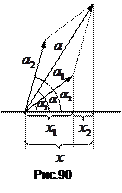 Розглянемо складання двох гармонічних коливань одного напрямку і частоти
Розглянемо складання двох гармонічних коливань одного напрямку і частоти
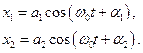
Представимо обидва коливання за допомогою векторів 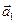 і
і 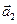 (рис.90). За правилом складання векторів побудуємо результуючий вектор
(рис.90). За правилом складання векторів побудуємо результуючий вектор 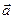 . Легко бачити, що результуючий рух
. Легко бачити, що результуючий рух 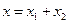 буде гармонічним коливанням з частотою
буде гармонічним коливанням з частотою 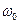 , амплітудою
, амплітудою 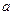 і початковою фазою
і початковою фазою 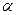 , тобто
, тобто
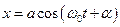 .
.
Амплітуда 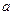 і початкова фаза
і початкова фаза 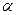 визначаються із трикутника на рис.90
визначаються із трикутника на рис.90
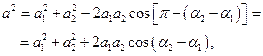
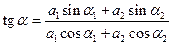 .
.
Такий спосіб складання коливань шляхом складання векторів застосовується, наприклад, в оптиці. Світлові коливання в деякій точці простору визначаються як результат накладання коливань, які приходять в цю точку від різних ділянок хвильового фронту.
Проаналізуємо вираз для амплітуди. Якщо різниця фаз обох коливань 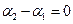 , то амплітуда результуючого коливання дорівнює сумі амплітуд
, то амплітуда результуючого коливання дорівнює сумі амплітуд 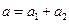 , а якщо різниця фаз
, а якщо різниця фаз 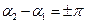 , тобто коли обидва коливання відбуваються в протифазі, то амплітуда результуючого коливання дорівнює
, тобто коли обидва коливання відбуваються в протифазі, то амплітуда результуючого коливання дорівнює 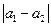 .
.
При складанні коливань різних частот результуючий рух буде не гармонічним коливанням, а складним коливальним процесом.
Биття
Цікавим виявляється випадок складання двох гармонічних коливань однакового напрямку, коли частоти їх слабо відрізняються. Покажемо, що результуюче коливання за таких умов уявляє собою гармонічне коливання з пульсуючою амплітудою. Таке коливання називається биттям.
Нехай частота одного коливання 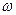 , а другого
, а другого 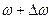 . Для спрощення задачі будемо вважати, що амплітуди обох коливань однакові, а початкові фази рівні нулю. Маємо
. Для спрощення задачі будемо вважати, що амплітуди обох коливань однакові, а початкові фази рівні нулю. Маємо
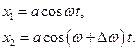
Результатом додавання цих функцій є вираз
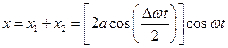 .
.
В аргументі другого множника знехтували членом 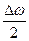 порівняно з
порівняно з 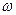 . Множник в квадратних дужках повільно змінюється з часом
. Множник в квадратних дужках повільно змінюється з часом 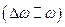 . Отже, можна вважати, що рівняння описує гармонічне коливання з частотою
. Отже, можна вважати, що рівняння описує гармонічне коливання з частотою 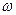 , амплітуда якого повільно змінюється. Графік функції для співвідношення
, амплітуда якого повільно змінюється. Графік функції для співвідношення 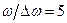 приведений на рис.91.
приведений на рис.91.
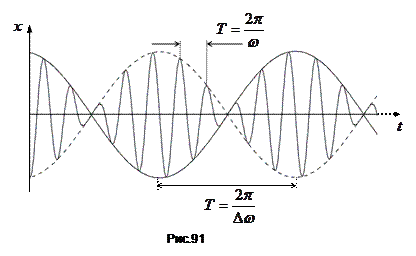
Період зміни амплітуди, як бачимо, вдвічі менший ніж період функції, що стоїть в квадратних дужках виразу . Тобто амплітудою треба вважати модуль цієї функції 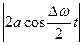 .
.
Дата добавления: 2015-06-17; просмотров: 967;
