Малі коливання

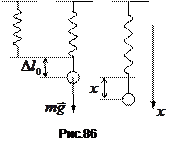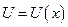Розглянемо систему з одною ступінню вільності (наприклад, кулька підвішена на пружині, рис.86). Потенціальна енергія системи . Домовимося відраховувати потенціальну енергію від положення рівноваги системи, тобто 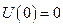. В стані стійкої рівноваги 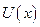має мінімум, а тому при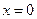 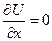. Розкладемо 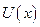в ряд Маклорена. Знехтувавши членами більш високого порядку малості ніж 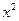, маємо

.

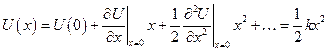Скориставшись співвідношенням (6.15) одержимо вираз для сили

,

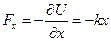який тотожній до виразу пружньої сили деформованої пружини, 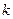– коефіцієнт пружності.

В положенні рівноваги сила тяжіння зрівноважена пружньою силою: 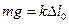. На відхилену на відстань від положення рівноваги кулю діє та ж сила тяжіння і пружня сила 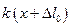. Рух кульки описується рівнянням другого закону Ньютона

.

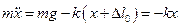Позначивши 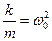, отримаємо рівняння гармонічних коливань

.

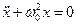Якщо врахувати сили опору середовища, вважаючи, як це часто має місце, що вони пропорційні величині швидкості 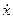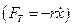, тоді рівняння другого закону Ньютона має вигляд

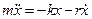
тут 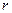– коефіцієнт опору. Позначивши 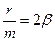, де 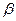– коефіцієнт затухання, отримаємо рівняння затухаючих коливань

.

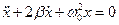Припустимо далі, що кулька знаходиться під впливом зовнішньої сили, що змінюється по гармонічному закону 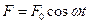. Тоді рівняння другого закону Ньютона матиме вигляд

.

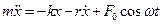Позначивши 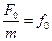, одержимо рівняння, яке описує вимушені коливання

.

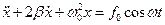Рівняння такого типу є лінійними диференційними рівняннями із сталими коефіцієнтами. Розв’язок- полегшується, якщо перейти до комплексних чисел. Тому згадаємо спочатку деякі властивості комплексних величин.

Комплексним числом називається число вигляду

,

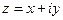де – дійсна частина комплексного числа, а 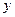– уявна частина 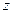; 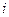– уявна одиниця 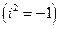. Число

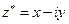
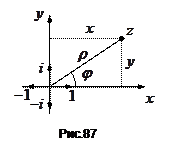називається комплексно спряженим числу 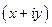. Комплексному числу можна спів ставити точку на площині (рис.87), з координатними осями і 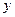. Але те ж саме число можна задати полярними координатами 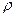і 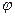. Використовуючи зв’язок між обома парами координат

, , , ,

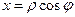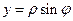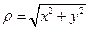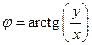можна представити комплексне число у вигляді

,

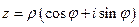або, скориставшись формулою Ейлера

,

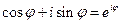отримаємо

.

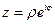Це так звана показникова форма комплексного числа. 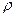і 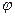– модуль і аргумент комплексного числа. Замінивши в формулі Ейлер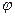а на 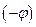прийдемо до співвідношення

,

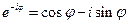яке дозволяє комплексно спряжене число 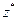в показниковій формі записати у вигляді

.

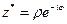Склавши вирази і отримаємо

.

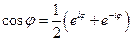Очевидно, що .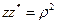

Із виразів і випливає, що при умові 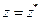, уявна частина комплексного числа дорівнює нулю. Це і є умова того, що комплексне число буде дійсним.

Як відомо з теорії, розв’язок диференціального рівняння другого порядку з сталими коефіцієнтами складається із суми загального розв’язку однорідного рівняння

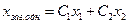
(тут 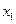і 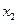– лінійно незалежні розв’язки однорідного рівняння, 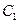і – довільні сталі) і окремого розв’язку неоднорідного рівняння

.

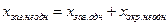Якщо припустити, що права частина рівняння комплексна і дорівнює 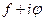, то і розв’язок цього рівняння буде комплексним числом 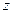, тобто 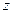задовольнятиме рівнянню

.

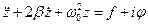Підставивши 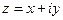в останнє рівняння і прирівнявши окремо дійсні і уявні частини в , отримаємо два незалежних рівняння

, .

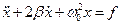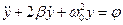Перше із цих рівнянь співпадає саме з рівнянням , розв’язок якого ми розшукуємо. Така властивість рівняння дозволяє в розв’язуванні застосувати наступний прийом. В рівнянні до правої частини, яка є дійсним числом 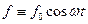, треба додати довільну уявну функцію. Із знайденого потім комплексного розв’язку треба виділити його дійсну частину, яка саме і буде розв’язком рівняння .