Застосування законів збереження до опису руху частинки в центральному полі сил
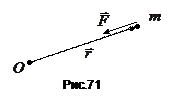 Центральним полем є поле, в якому сила
Центральним полем є поле, в якому сила 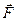 за абсолютною величиною залежить тільки від відстані
за абсолютною величиною залежить тільки від відстані  до деякої певної точки
до деякої певної точки 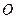 (центра) в просторі. Направлена сила вздовж прямої, що з’єднує досліджувану частинку масою
(центра) в просторі. Направлена сила вздовж прямої, що з’єднує досліджувану частинку масою 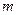 з центром (рис.71)
з центром (рис.71)
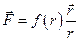 .
.
1. Поле центральних сил консервативне, тому повна механічна енергія 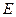 частинки
частинки 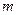 зберігається
зберігається
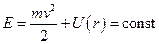 .
.
2. Імпульс частинки 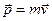 не зберігається, оскільки
не зберігається, оскільки 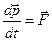 .
.
3. Момент імпульсу  частинки
частинки 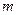 , визначений не відносно довільної точки простору, а саме відносно центра поля
, визначений не відносно довільної точки простору, а саме відносно центра поля 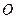 , зберігається
, зберігається
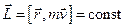 , оскільки
, оскільки  .
.
Таким чином, зберігаються з часом величини 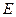 і
і  . Зробимо висновки.
. Зробимо висновки.
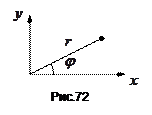 Як вже було сказано
Як вже було сказано 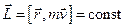 . Зауважимо, що момент імпульсу залишається сталим і за величиною і за напрямком. Оскільки
. Зауважимо, що момент імпульсу залишається сталим і за величиною і за напрямком. Оскільки 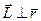 і
і 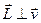 , то внаслідок сталості напрямку
, то внаслідок сталості напрямку  при русі частинки її радіус-вектор
при русі частинки її радіус-вектор 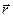 весь час залишається в одній площині – площині, перпендикулярній до вектора
весь час залишається в одній площині – площині, перпендикулярній до вектора  . Таким чином, перший висновок полягає в тому, що траєкторія руху частинки в центральному полі цілком лежить в одній площині. Виберемо декартову систему координат так, щоб вектор
. Таким чином, перший висновок полягає в тому, що траєкторія руху частинки в центральному полі цілком лежить в одній площині. Виберемо декартову систему координат так, щоб вектор  співпадав з напрямом осі
співпадав з напрямом осі 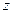 :
: 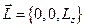 . Тоді частинка рухається в площині
. Тоді частинка рухається в площині 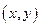 .
.
Перейдемо до полярної системи координат 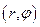 . Як видно з рис.72, зв’язок полярних з декартовими координатами такий
. Як видно з рис.72, зв’язок полярних з декартовими координатами такий
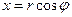 ,
,
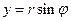 .
.
Диференціюючи останні рівняння по часу одержимо
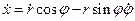 ,
,
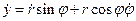 .
.
Знайдемо вираз  в полярній системі координат
в полярній системі координат
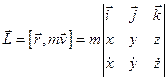 .
.
Оскільки 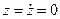 , тоді проекції
, тоді проекції 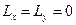 . Запишемо проекцію
. Запишемо проекцію 
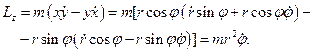
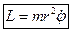
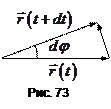 Бачимо, що
Бачимо, що 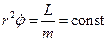 , оскільки
, оскільки 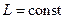 і
і 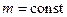 . Але величина
. Але величина 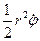 є так звана секторіальна швидкість
є так звана секторіальна швидкість 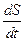 (площа сектора, що утворюється двома нескінченно близькими радіусами-векторами і елементом дуги траєкторії). Її легко знайти з рис.73
(площа сектора, що утворюється двома нескінченно близькими радіусами-векторами і елементом дуги траєкторії). Її легко знайти з рис.73
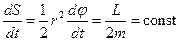 .
.
Тому другий висновок, який випливає із сталості моменту імпульсу, стверджує про те, що частинка буде рухатись із сталою секторіальною швидкістю (другий закон Кеплера).
Розглянемо в полярній системі координат вираз повної енергії частинки 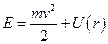
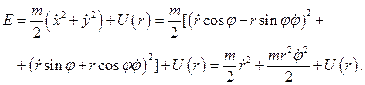
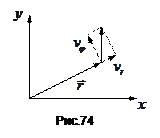 Тут
Тут  – радіальна швидкість ,
– радіальна швидкість ,  – азимутальна швидкість (рис.74). Якщо виразити
– азимутальна швидкість (рис.74). Якщо виразити 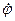 через
через 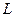 за допомогою рівняння
за допомогою рівняння 
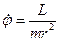 ,
,
і підставити у вираз для енергії, то одержимо
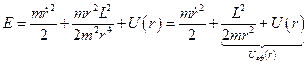 .
.
Останній вираз показує, що рух частинки вздовж радіуса 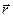 (радіальна частина руху) можна розглядати як одномірний рух частинки у потенціальному силовому полі, яке описується ефективною потенціальною енергією
(радіальна частина руху) можна розглядати як одномірний рух частинки у потенціальному силовому полі, яке описується ефективною потенціальною енергією
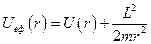 .
.
Повний рух частинки можна уявити як такий, коли частинка рухається вздовж радіуса-вектора 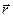 , а сам
, а сам 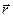 повертається.
повертається.
Розв’язуючи рівняння відносно 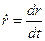 і відокремлюючи змінні, маємо
і відокремлюючи змінні, маємо
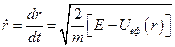 ,
,
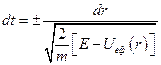 ,
,
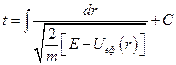 .
.
Дістаємо рівняння, яке визначає залежність 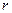 від часу
від часу
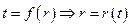 .
.
Сталі 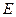 і
і 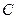 визначають за початковими значеннями координати і швидкості частинки.
визначають за початковими значеннями координати і швидкості частинки.
За аналогією з аналізом одномірного руху частинки, дістаємо нерівність
 ,
,
яка визначає області зміни довжини радіуса-вектора 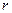 частинки та можливі значення повної енергії
частинки та можливі значення повної енергії 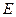 . Для існування розв’язку рівняння необхідно, щоб повна енергія була більшою за найменше можливе значення ефективної потенціальної енергії
. Для існування розв’язку рівняння необхідно, щоб повна енергія була більшою за найменше можливе значення ефективної потенціальної енергії 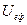 . Рівняння
. Рівняння
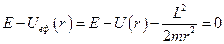 .
.
визначає значення 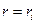 , що відповідають точкам повороту. Оскільки при реальному русі частинки змінюється не тільки довжина
, що відповідають точкам повороту. Оскільки при реальному русі частинки змінюється не тільки довжина 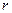 , а і кут
, а і кут 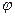 , то точки повороту в розглядуваному випадку не є точками зупинки частинки. Її швидкість в цих точках не обертається в нуль.
, то точки повороту в розглядуваному випадку не є точками зупинки частинки. Її швидкість в цих точках не обертається в нуль.
Щоб знайти залежність кута 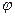 від часу, використаємо рівняння, яке визначає собою закон збереження моменту імпульсу
від часу, використаємо рівняння, яке визначає собою закон збереження моменту імпульсу
 .
.
Якщо вважати 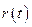 відомою функцією часу, шляхом інтегрування виразу
відомою функцією часу, шляхом інтегрування виразу 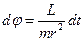 знайдемо
знайдемо 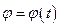 .
.
Отже, знайдені
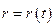 ,
,
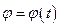 .
.
Шляхом виключення часу 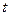 з останніх двох рівнянь знайдемо траєкторію частинки
з останніх двох рівнянь знайдемо траєкторію частинки
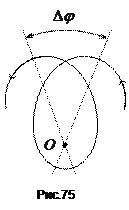
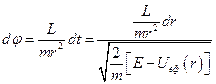 .
.
Далі, інтегруючи, маємо
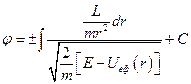 .
.
Для випадку фінітного руху, коли траєкторія частинки лежить в обмеженій області площини  , тобто коли
, тобто коли 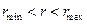 , радіальний рух завжди періодичний. Період цього руху можна визначити за формулою
, радіальний рух завжди періодичний. Період цього руху можна визначити за формулою
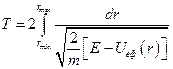 ,
,
де 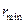 і
і 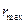 визначаються рівняннями .
визначаються рівняннями .
Для того, щоб рух частинки в цілому був періодичний, необхідно, щоб за ціле число періодів радіального руху 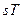 кут
кут 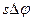 описав ціле число циклів
описав ціле число циклів 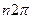 (рис.75). Тобто умовою періодичності буде
(рис.75). Тобто умовою періодичності буде 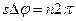 . Тут
. Тут 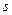 і
і 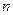 цілі числа. Ця умова і є умовою замкнутості траєкторії частинки при фінітному русі. Взагалі кажучи, ця умова для певної функції
цілі числа. Ця умова і є умовою замкнутості траєкторії частинки при фінітному русі. Взагалі кажучи, ця умова для певної функції 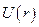 виконується тільки при певних значеннях сталих
виконується тільки при певних значеннях сталих 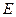 і
і 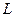 . Але можна показати, що існують лише два центральних поля
. Але можна показати, що існують лише два центральних поля 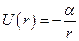 і
і 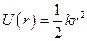 (тут
(тут 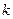 і
і 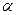 – додатні сталі), для яких траєкторії частинок при фінітному русі завжди будуть замкнутими кривими. Фінітний чи інфінітний рухи буде виконувати частинка буде залежати від конкретного вигляду
– додатні сталі), для яких траєкторії частинок при фінітному русі завжди будуть замкнутими кривими. Фінітний чи інфінітний рухи буде виконувати частинка буде залежати від конкретного вигляду 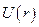 .
.
Приклади:
 1. Нехай
1. Нехай 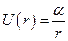 ,
, 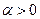 . Тоді
. Тоді 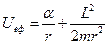 (рис.76),
(рис.76),
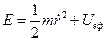 .
.
Область дозволених значень 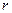 визначається умовою
визначається умовою 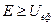 , в даному випадку
, в даному випадку 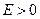 .
.
Так відбувається розсіяння (відштовхування) точки на силовому центрі.
2. Нехай 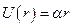 ,
, 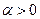 . Тоді
. Тоді 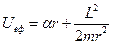 (рис.77, а). Область дозволених значень
(рис.77, а). Область дозволених значень 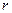 визначається умовою
визначається умовою
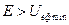
Тут буде відбуватися фінітний рух. Траєкторія показана на рис.77, б. 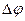 – кут повороту орбіти за період радіального руху.
– кут повороту орбіти за період радіального руху.
Дата добавления: 2015-06-17; просмотров: 1880;
