Резонанси в системі з двома ступенями свободи. Фільтри

Розглянемо вимушені коливання системи з двома ступенями свободи. У цьому випадку на точки системи, крім сил, що мають потенціал, діє возмущающие сили 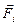, які є деякими заданими функціями часу 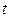. Рівняння Лагранжа для даної системи мають вигляд

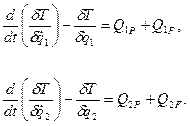(4.17)

Приймаємо, що узагальнені возмущающие сили 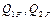є простими гармонійними функціями часу, що мають однакову частоту 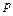і фазу 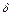, тобто

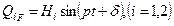. (4.18)

Тоді диференціальні рівняння вимушених коливань цієї системи мають вигляд

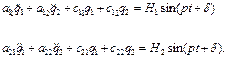(4.19)

Загальний інтеграл системи однорідних рівнянь, відповідних (4.19), вже нам відомий і характеризує вільні коливання системи (див. 4.12).

Приватні рішення системи (4.19) будемо шукати у вигляді

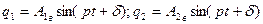. (4.20)

Підставляючи (4.20) в рівняння (4.19) і скорочуючи на 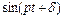, отримуємо

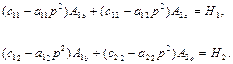(4.21)

З цієї системи маємо наступні вирази для амплітуд вимушених коливань:

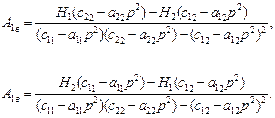(4.22)

.

Підставивши (4.22) в рівняння (4.20) встановлюємо наступне:

1. Вимушені коливання системи є гармонійними і мають частоту і фазу збурюючих сил.

2. Амплітуди вимушених коливань системи не залежать від початкових умов і визначається тільки властивостями системи і діють на них силами.

Загальні інтеграли диференціальних рівнянь (4.19) тепер мають вигляд:

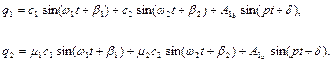
При цьому частоти 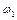і і 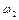коефіцієнти розподілу 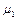і 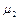нам уже відомі (див. (4.8), (4.9)). Так як знаменник у виразах для амплітуд (4.22) 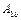, 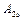є квадратним многочленом відносно 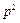, а корені цього многочлена є квадрати частот головних коливань системи 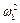і 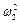, то формули (4.22) можна представити у вигляді

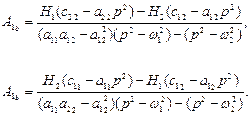(4.23)

При 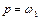бо 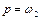амплітуди 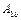і 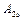зі збільшенням часу необмежено зростають, тобто маємо явище резонансу.

У разі резонансу вираз (4.20) не є окремим рішенням системи диференціальних рівнянь вимушених коливань (4.19).

Для отримання приватного рішення у разі резонансу скористаємося головними координатами системи 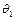і .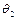

Диференціальні рівняння вимушених коливань системи мають такий вигляд:

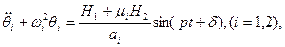(4.24)

де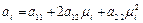

Приватні рішення рівнянь (4.19) тепер мають вигляд

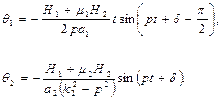(4.25)

Переходячи до узагальнених координат 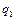і 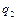отримуємо, наприклад для :

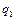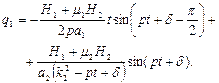(4.26)

Висновок: наведене рівняння (4.26) показує, що у разі резонансу у вирази узагальнених координат входять члени, що містять час 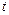у вигляді множника перед тригонометричною функцією. Зі збільшенням часу ці члени необмежено зростають, що і відповідає явищу резонансу.

Визначимо тепер відношення амплітуд вимушених коливань

,

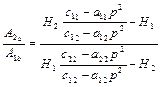яке при 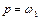і 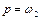зберігає кінцеве значення і дорівнює:

при ,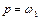

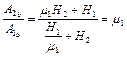при .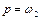

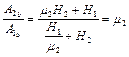Висновок: отримані співвідношення показують, що у разі резонансу форми вимушених коливань системи аналогічні відповідним формам головних коливань.

Динамічний гаситель коливань (фільтр).

Розглянемо випадок, коли одна з узагальнених збурюючих сил дорівнює нулю. Покладемо, що

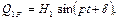а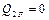

Тоді при 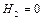вираження амплітуд вимушених коливань (4.23) спрощуються і при 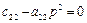, тобто при 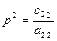маємо

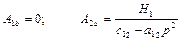
Висновок: таким чином при 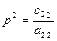вимушені коливання, що відповідають першій узагальненій координаті, повністю гасяться.

На цьому принципі заснована теорія динамічних гасителів (фільтрів).

КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 4

1. Які системи називаються парціальними системами?

2. Наведіть приклади неоднозначного вибору парціальних систем для даної складної системи.

3. Розв'яжіть рівняння (4.8) для власних частот системи і побудуйте графік (так званий графік Вина) їх зміни від співвідношення парціальних частот. Обговоріть результати.

4. Поясніть принцип роботи динамічних гасителів.

5. Отримайте квадратичні форми кінетичної і потенційної 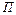енергій для систем з двома ступенями свободи.